Question Number 163574 by Zaynal last updated on 08/Jan/22
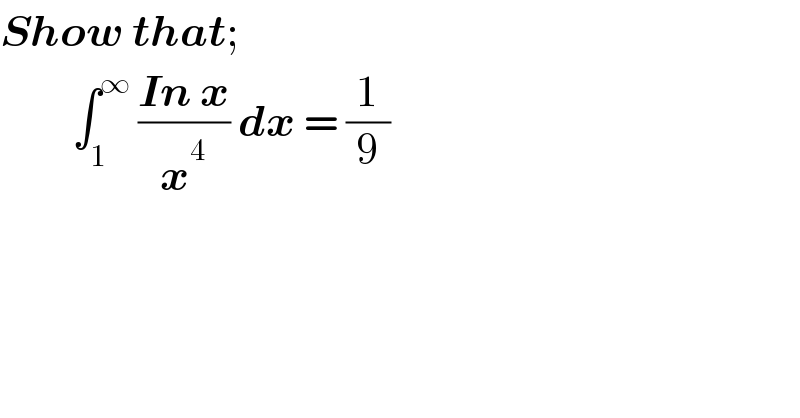
$$\boldsymbol{{Show}}\:\boldsymbol{{that}}; \\ $$$$\:\:\:\:\:\:\:\:\:\int_{\mathrm{1}} ^{\infty} \:\frac{\boldsymbol{{In}}\:\boldsymbol{{x}}}{\boldsymbol{{x}}^{\mathrm{4}} }\:\boldsymbol{{dx}}\:=\:\frac{\mathrm{1}}{\mathrm{9}} \\ $$
Answered by Ar Brandon last updated on 08/Jan/22
![∫_1 ^∞ ((lnx)/x^4 )dx=(∂/∂α)∣_(α=0) ∫_1 ^∞ (x^α /x^4 )dx=(∂/∂α)∣_(α=0) [(x^(α−3) /(α−3))]_1 ^∞ =(∂/∂α)∣_(α=0) (1/(3−α))=∣_(α=0) (1/((3−α)^2 ))=(1/3^2 )=(1/9)](https://www.tinkutara.com/question/Q163592.png)
$$\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{ln}{x}}{{x}^{\mathrm{4}} }{dx}=\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{0}} \int_{\mathrm{1}} ^{\infty} \frac{{x}^{\alpha} }{{x}^{\mathrm{4}} }{dx}=\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{0}} \left[\frac{{x}^{\alpha−\mathrm{3}} }{\alpha−\mathrm{3}}\right]_{\mathrm{1}} ^{\infty} \\ $$$$=\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{0}} \frac{\mathrm{1}}{\mathrm{3}−\alpha}=\mid_{\alpha=\mathrm{0}} \frac{\mathrm{1}}{\left(\mathrm{3}−\alpha\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{9}} \\ $$
