Menu Close

a-2-a-3b-b-2-b-3a-27-ab-2-find-a-3-b-3-

Tinku Tara 0 Comments
Pin




Question Number 163747 by HongKing last updated on 10/Jan/22
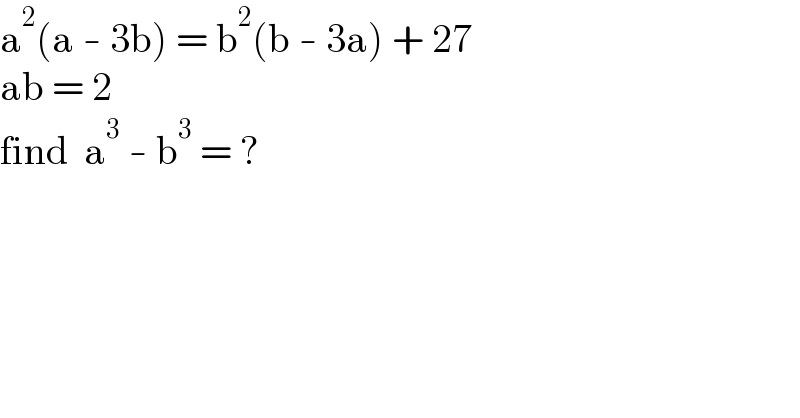
a^2 (a - 3b) = b^2 (b - 3a) + 27 ab = 2 find a^3 - b^3 = ?
$$\mathrm{a}^{\mathrm{2}} \left(\mathrm{a}\:-\:\mathrm{3b}\right)\:=\:\mathrm{b}^{\mathrm{2}} \left(\mathrm{b}\:-\:\mathrm{3a}\right)\:+\:\mathrm{27} \\ $$$$\mathrm{ab}\:=\:\mathrm{2} \\ $$$$\mathrm{find}\:\:\mathrm{a}^{\mathrm{3}} \:-\:\mathrm{b}^{\mathrm{3}} \:=\:? \\ $$
Answered by nurtani last updated on 10/Jan/22
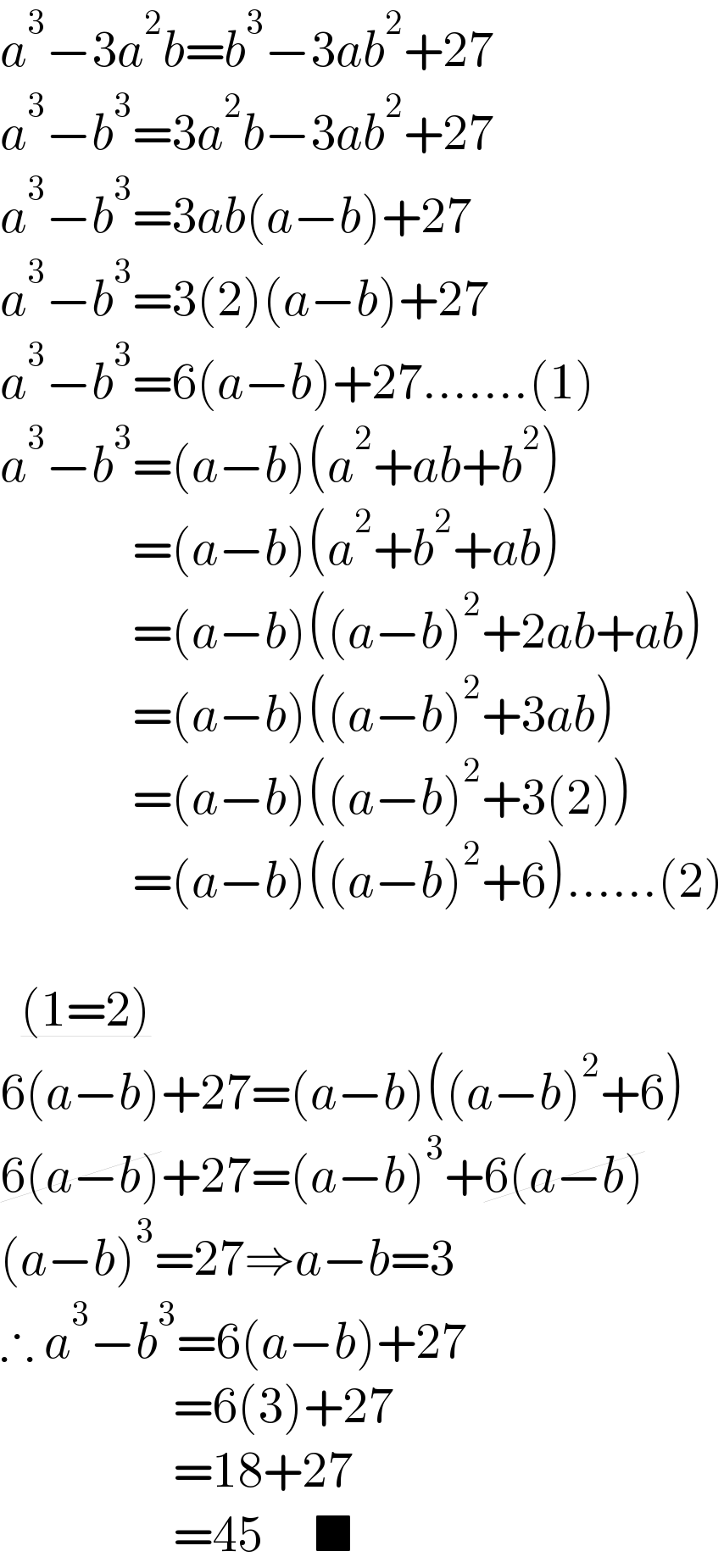
a^3 −3a^2 b=b^3 −3ab^2 +27 a^3 −b^3 =3a^2 b−3ab^2 +27 a^3 −b^3 =3ab(a−b)+27 a^3 −b^3 =3(2)(a−b)+27 a^3 −b^3 =6(a−b)+27.......(1) a^3 −b^3 =(a−b)(a^2 +ab+b^2 ) =(a−b)(a^2 +b^2 +ab) =(a−b)((a−b)^2 +2ab+ab) =(a−b)((a−b)^2 +3ab) =(a−b)((a−b)^2 +3(2)) =(a−b)((a−b)^2 +6)......(2) (1=2) 6(a−b)+27=(a−b)((a−b)^2 +6) 6(a−b)+27=(a−b)^3 +6(a−b) (a−b)^3 =27⇒a−b=3 ∴ a^3 −b^3 =6(a−b)+27 =6(3)+27 =18+27 =45 ■
$${a}^{\mathrm{3}} −\mathrm{3}{a}^{\mathrm{2}} {b}={b}^{\mathrm{3}} −\mathrm{3}{ab}^{\mathrm{2}} +\mathrm{27} \\ $$$${a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\mathrm{3}{a}^{\mathrm{2}} {b}−\mathrm{3}{ab}^{\mathrm{2}} +\mathrm{27} \\ $$$${a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\mathrm{3}{ab}\left({a}−{b}\right)+\mathrm{27} \\ $$$${a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\mathrm{3}\left(\mathrm{2}\right)\left({a}−{b}\right)+\mathrm{27} \\ $$$${a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\mathrm{6}\left({a}−{b}\right)+\mathrm{27}…….\left(\mathrm{1}\right) \\ $$$${a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\left({a}−{b}\right)\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({a}−{b}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{ab}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({a}−{b}\right)\left(\left({a}−{b}\right)^{\mathrm{2}} +\mathrm{2}{ab}+{ab}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({a}−{b}\right)\left(\left({a}−{b}\right)^{\mathrm{2}} +\mathrm{3}{ab}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({a}−{b}\right)\left(\left({a}−{b}\right)^{\mathrm{2}} +\mathrm{3}\left(\mathrm{2}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({a}−{b}\right)\left(\left({a}−{b}\right)^{\mathrm{2}} +\mathrm{6}\right)……\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\:\:\underline{\left(\mathrm{1}=\mathrm{2}\right)}\:\:\:\: \\ $$$$\mathrm{6}\left({a}−{b}\right)+\mathrm{27}=\left({a}−{b}\right)\left(\left({a}−{b}\right)^{\mathrm{2}} +\mathrm{6}\right) \\ $$$$\cancel{\mathrm{6}\left({a}−{b}\right)}+\mathrm{27}=\left({a}−{b}\right)^{\mathrm{3}} +\cancel{\mathrm{6}\left({a}−{b}\right)} \\ $$$$\left({a}−{b}\right)^{\mathrm{3}} =\mathrm{27}\Rightarrow{a}−{b}=\mathrm{3} \\ $$$$\therefore\:{a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\mathrm{6}\left({a}−{b}\right)+\mathrm{27} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{6}\left(\mathrm{3}\right)+\mathrm{27} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{18}+\mathrm{27} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{45}\:\:\:\:\:\blacksquare \\ $$
Answered by Rasheed.Sindhi last updated on 10/Jan/22
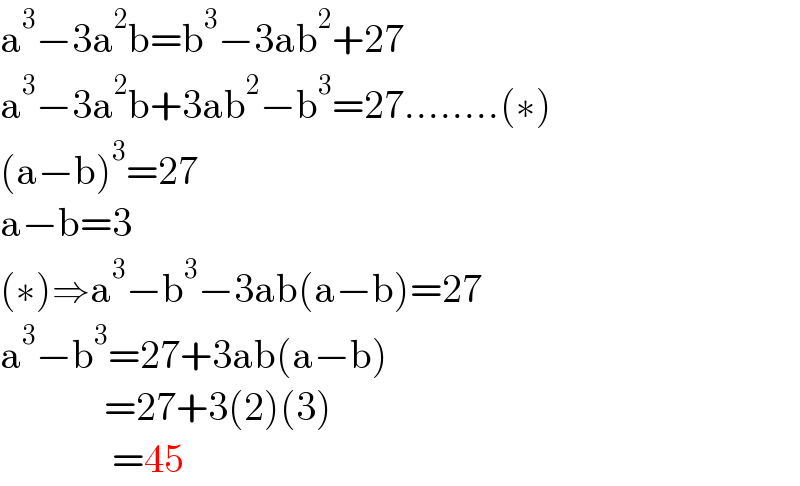
a^3 −3a^2 b=b^3 −3ab^2 +27 a^3 −3a^2 b+3ab^2 −b^3 =27........(∗) (a−b)^3 =27 a−b=3 (∗)⇒a^3 −b^3 −3ab(a−b)=27 a^3 −b^3 =27+3ab(a−b) =27+3(2)(3) =45
$$\mathrm{a}^{\mathrm{3}} −\mathrm{3a}^{\mathrm{2}} \mathrm{b}=\mathrm{b}^{\mathrm{3}} −\mathrm{3ab}^{\mathrm{2}} +\mathrm{27} \\ $$$$\mathrm{a}^{\mathrm{3}} −\mathrm{3a}^{\mathrm{2}} \mathrm{b}+\mathrm{3ab}^{\mathrm{2}} −\mathrm{b}^{\mathrm{3}} =\mathrm{27}……..\left(\ast\right) \\ $$$$\left(\mathrm{a}−\mathrm{b}\right)^{\mathrm{3}} =\mathrm{27} \\ $$$$\mathrm{a}−\mathrm{b}=\mathrm{3} \\ $$$$\left(\ast\right)\Rightarrow\mathrm{a}^{\mathrm{3}} −\mathrm{b}^{\mathrm{3}} −\mathrm{3ab}\left(\mathrm{a}−\mathrm{b}\right)=\mathrm{27} \\ $$$$\mathrm{a}^{\mathrm{3}} −\mathrm{b}^{\mathrm{3}} =\mathrm{27}+\mathrm{3ab}\left(\mathrm{a}−\mathrm{b}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{27}+\mathrm{3}\left(\mathrm{2}\right)\left(\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{45} \\ $$
Commented by HongKing last updated on 10/Jan/22
very nice my dear Sir thank you
$$\mathrm{very}\:\mathrm{nice}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *