Menu Close

solve-x-y-N-3x-5y-20-

Tinku Tara 0 Comments
Pin




Question Number 163770 by mnjuly1970 last updated on 10/Jan/22
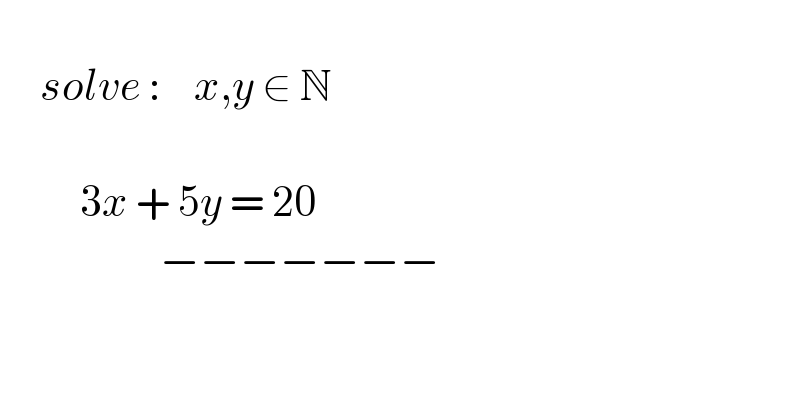
solve : x,y ∈ N 3x + 5y = 20 −−−−−−−
$$ \\ $$$$\:\:\:\:\:{solve}\::\:\:\:\:{x},{y}\:\in\:\mathbb{N}\: \\ $$$$\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{3}{x}\:+\:\mathrm{5}{y}\:=\:\mathrm{20}\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−−−−− \\ $$
Answered by MJS_new last updated on 10/Jan/22
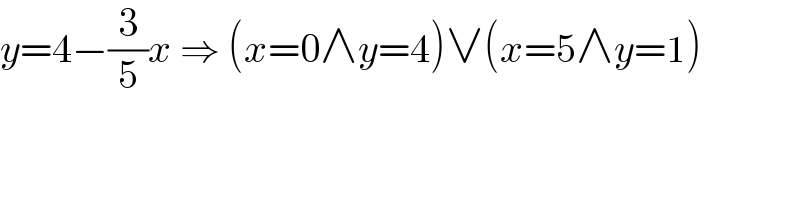
y=4−(3/5)x ⇒ (x=0∧y=4)∨(x=5∧y=1)
$${y}=\mathrm{4}−\frac{\mathrm{3}}{\mathrm{5}}{x}\:\Rightarrow\:\left({x}=\mathrm{0}\wedge{y}=\mathrm{4}\right)\vee\left({x}=\mathrm{5}\wedge{y}=\mathrm{1}\right) \\ $$
Commented by MJS_new last updated on 10/Jan/22
yes, thank you!
$$\mathrm{yes},\:\mathrm{thank}\:\mathrm{you}! \\ $$
Commented by MathsFan last updated on 10/Jan/22
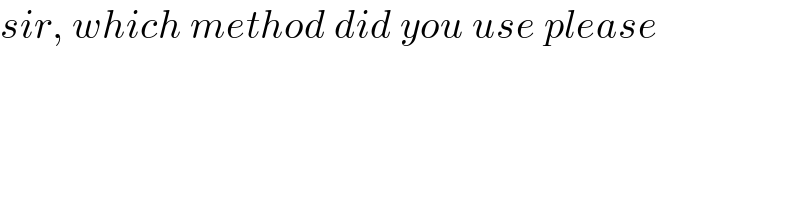
sir, which method did you use please
$${sir},\:{which}\:{method}\:{did}\:{you}\:{use}\:{please} \\ $$
Commented by MJS_new last updated on 10/Jan/22
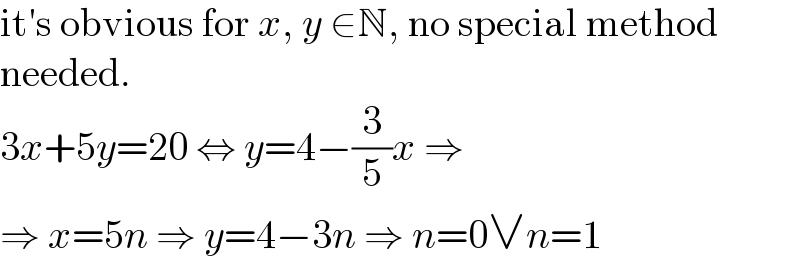
it′s obvious for x, y ∈N, no special method needed. 3x+5y=20 ⇔ y=4−(3/5)x ⇒ ⇒ x=5n ⇒ y=4−3n ⇒ n=0∨n=1
$$\mathrm{it}'\mathrm{s}\:\mathrm{obvious}\:\mathrm{for}\:{x},\:{y}\:\in\mathbb{N},\:\mathrm{no}\:\mathrm{special}\:\mathrm{method} \\ $$$$\mathrm{needed}. \\ $$$$\mathrm{3}{x}+\mathrm{5}{y}=\mathrm{20}\:\Leftrightarrow\:{y}=\mathrm{4}−\frac{\mathrm{3}}{\mathrm{5}}{x}\:\Rightarrow \\ $$$$\Rightarrow\:{x}=\mathrm{5}{n}\:\Rightarrow\:{y}=\mathrm{4}−\mathrm{3}{n}\:\Rightarrow\:{n}=\mathrm{0}\vee{n}=\mathrm{1} \\ $$
Answered by Mathspace last updated on 10/Jan/22
we consider congruence modulo3 e ⇒3^. x^. +5^. y^. =(20)^. ⇒ 0+2^. y^. =2^. ⇒y^. =1^. ⇒y=3k+1 3x=20−5y =20−5(3k+1) =15−15k (k∈Z) rememeber thst Z/3Z est un corps
$${we}\:{consider}\:{congruence}\:{modulo}\mathrm{3} \\ $$$${e}\:\Rightarrow\overset{.} {\mathrm{3}}\overset{.} {{x}}\:+\overset{.} {\mathrm{5}}\overset{.} {{y}}\:=\left(\mathrm{20}\overset{.} {\right)}\:\Rightarrow \\ $$$$\mathrm{0}+\overset{.} {\mathrm{2}}\overset{.} {{y}}=\overset{.} {\mathrm{2}}\:\:\Rightarrow\overset{.} {{y}}=\overset{.} {\mathrm{1}}\:\Rightarrow{y}=\mathrm{3}{k}+\mathrm{1} \\ $$$$\mathrm{3}{x}=\mathrm{20}−\mathrm{5}{y}\:=\mathrm{20}−\mathrm{5}\left(\mathrm{3}{k}+\mathrm{1}\right) \\ $$$$=\mathrm{15}−\mathrm{15}{k}\:\:\:\left({k}\in{Z}\right) \\ $$$${rememeber}\:{thst}\:{Z}/\mathrm{3}{Z}\:\:{est}\:{un}\:{corps} \\ $$
Commented by Mathspace last updated on 10/Jan/22
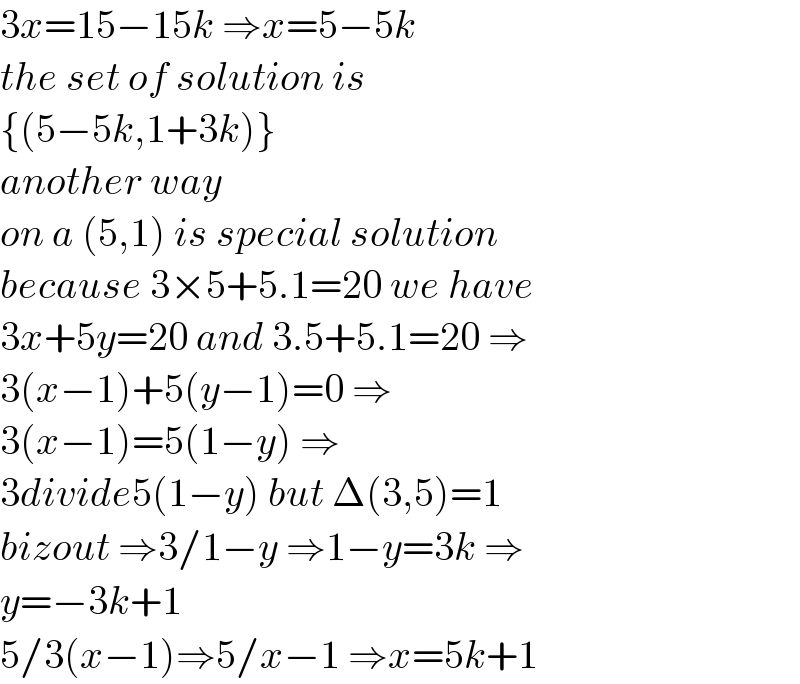
3x=15−15k ⇒x=5−5k the set of solution is {(5−5k,1+3k)} another way on a (5,1) is special solution because 3×5+5.1=20 we have 3x+5y=20 and 3.5+5.1=20 ⇒ 3(x−1)+5(y−1)=0 ⇒ 3(x−1)=5(1−y) ⇒ 3divide5(1−y) but Δ(3,5)=1 bizout ⇒3/1−y ⇒1−y=3k ⇒ y=−3k+1 5/3(x−1)⇒5/x−1 ⇒x=5k+1
$$\mathrm{3}{x}=\mathrm{15}−\mathrm{15}{k}\:\Rightarrow{x}=\mathrm{5}−\mathrm{5}{k} \\ $$$${the}\:{set}\:{of}\:{solution}\:{is} \\ $$$$\left\{\left(\mathrm{5}−\mathrm{5}{k},\mathrm{1}+\mathrm{3}{k}\right)\right\} \\ $$$${another}\:{way} \\ $$$${on}\:{a}\:\left(\mathrm{5},\mathrm{1}\right)\:{is}\:{special}\:{solution} \\ $$$${because}\:\mathrm{3}×\mathrm{5}+\mathrm{5}.\mathrm{1}=\mathrm{20}\:{we}\:{have} \\ $$$$\mathrm{3}{x}+\mathrm{5}{y}=\mathrm{20}\:{and}\:\mathrm{3}.\mathrm{5}+\mathrm{5}.\mathrm{1}=\mathrm{20}\:\Rightarrow \\ $$$$\mathrm{3}\left({x}−\mathrm{1}\right)+\mathrm{5}\left({y}−\mathrm{1}\right)=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{3}\left({x}−\mathrm{1}\right)=\mathrm{5}\left(\mathrm{1}−{y}\right)\:\Rightarrow \\ $$$$\mathrm{3}{divide}\mathrm{5}\left(\mathrm{1}−{y}\right)\:{but}\:\Delta\left(\mathrm{3},\mathrm{5}\right)=\mathrm{1} \\ $$$${bizout}\:\Rightarrow\mathrm{3}/\mathrm{1}−{y}\:\Rightarrow\mathrm{1}−{y}=\mathrm{3}{k}\:\Rightarrow \\ $$$${y}=−\mathrm{3}{k}+\mathrm{1} \\ $$$$\mathrm{5}/\mathrm{3}\left({x}−\mathrm{1}\right)\Rightarrow\mathrm{5}/{x}−\mathrm{1}\:\Rightarrow{x}=\mathrm{5}{k}+\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *