Question Number 68636 by ajfour last updated on 14/Sep/19
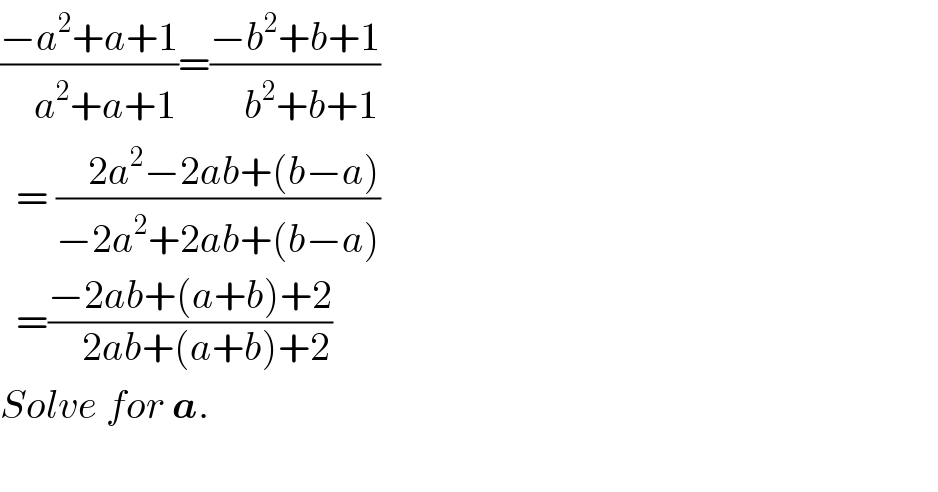
$$\frac{−{a}^{\mathrm{2}} +{a}+\mathrm{1}}{\:\:\:\:{a}^{\mathrm{2}} +{a}+\mathrm{1}}=\frac{−{b}^{\mathrm{2}} +{b}+\mathrm{1}}{\:\:\:\:{b}^{\mathrm{2}} +{b}+\mathrm{1}} \\ $$$$\:\:=\:\frac{\:\:\:\:\mathrm{2}{a}^{\mathrm{2}} −\mathrm{2}{ab}+\left({b}−{a}\right)}{−\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{ab}+\left({b}−{a}\right)} \\ $$$$\:\:=\frac{−\mathrm{2}{ab}+\left({a}+{b}\right)+\mathrm{2}}{\:\:\:\:\mathrm{2}{ab}+\left({a}+{b}\right)+\mathrm{2}} \\ $$$${Solve}\:{for}\:\boldsymbol{{a}}. \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 15/Sep/19

$$\frac{−{a}^{\mathrm{2}} +{a}+\mathrm{1}}{\:\:\:\:{a}^{\mathrm{2}} +{a}+\mathrm{1}}=\frac{−{b}^{\mathrm{2}} +{b}+\mathrm{1}}{\:\:\:\:{b}^{\mathrm{2}} +{b}+\mathrm{1}}………\left({i}\right) \\ $$$$\:\:\frac{−{a}^{\mathrm{2}} +{a}+\mathrm{1}}{\:\:\:\:{a}^{\mathrm{2}} +{a}+\mathrm{1}}=\frac{\:\:\:\:\mathrm{2}{a}^{\mathrm{2}} −\mathrm{2}{ab}+\left({b}−{a}\right)}{−\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{ab}+\left({b}−{a}\right)}…\left({ii}\right) \\ $$$$ \\ $$$$\frac{\left(−{a}^{\mathrm{2}} +{a}+\mathrm{1}\right)+\left({a}^{\mathrm{2}} +{a}+\mathrm{1}\right)}{\:\:\:\:{a}^{\mathrm{2}} +{a}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left(−{b}^{\mathrm{2}} +{b}+\mathrm{1}\right)+\left({b}^{\mathrm{2}} +{b}+\mathrm{1}\right)}{\:\:\:\:{b}^{\mathrm{2}} +{b}+\mathrm{1}} \\ $$$$\frac{\mathrm{2}{a}+\mathrm{2}}{\:\:\:\:{a}^{\mathrm{2}} +{a}+\mathrm{1}}=\frac{\mathrm{2}{b}+\mathrm{2}}{\:\:\:\:{b}^{\mathrm{2}} +{b}+\mathrm{1}} \\ $$$$\frac{{a}^{\mathrm{2}} +{a}+\mathrm{1}}{{a}+\mathrm{1}}=\frac{{b}^{\mathrm{2}} +{b}+\mathrm{1}}{{b}+\mathrm{1}} \\ $$$$\frac{{a}^{\mathrm{2}} }{{a}+\mathrm{1}}=\frac{{b}^{\mathrm{2}} }{{b}+\mathrm{1}} \\ $$$${a}^{\mathrm{2}} \left({b}+\mathrm{1}\right)−{b}^{\mathrm{2}} \left({a}+\mathrm{1}\right)=\mathrm{0} \\ $$$${a}^{\mathrm{2}} {b}+{a}^{\mathrm{2}} −{ab}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{0} \\ $$$${a}^{\mathrm{2}} {b}−{ab}^{\mathrm{2}} +{a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{0} \\ $$$${ab}\left({a}−{b}\right)+\left({a}+{b}\right)\left({a}−{b}\right)=\mathrm{0} \\ $$$$\left({a}−{b}\right)\left({a}+{ab}+{b}\right)=\mathrm{0} \\ $$$${a}={b}\:\:\mid\:\:\:{b}=−\frac{{a}}{{a}+\mathrm{1}} \\ $$$${a}={b}: \\ $$$$\left({ii}\right):\frac{−{a}^{\mathrm{2}} +{a}+\mathrm{1}}{\:\:\:\:{a}^{\mathrm{2}} +{a}+\mathrm{1}}=\frac{\:\:\:\:\mathrm{2}{a}^{\mathrm{2}} −\mathrm{2}{ab}+\left({b}−{a}\right)}{−\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{ab}+\left({b}−{a}\right)} \\ $$$$\:\:\:\:\:\:\frac{−{a}^{\mathrm{2}} +{a}+\mathrm{1}}{\:\:\:\:{a}^{\mathrm{2}} +{a}+\mathrm{1}}=\frac{\:\:\:\:\mathrm{2}{a}^{\mathrm{2}} −\mathrm{2}{a}.{a}+\left({a}−{a}\right)}{−\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{a}.{a}+\left({a}−{a}\right)} \\ $$$$\:\:\:\:\:\:\frac{−{a}^{\mathrm{2}} +{a}+\mathrm{1}}{\:\:\:\:{a}^{\mathrm{2}} +{a}+\mathrm{1}}=\frac{\mathrm{0}}{\mathrm{0}}\:\left({Indeterminate}\right) \\ $$$${b}=−\frac{{a}}{{a}+\mathrm{1}} \\ $$$$\left({ii}\right):\frac{−{a}^{\mathrm{2}} +{a}+\mathrm{1}}{\:\:\:\:{a}^{\mathrm{2}} +{a}+\mathrm{1}}=\frac{\:\:\:\:\mathrm{2}{a}^{\mathrm{2}} −\mathrm{2}{ab}+\left({b}−{a}\right)}{−\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{ab}+\left({b}−{a}\right)} \\ $$$$\Rightarrow\frac{−{a}^{\mathrm{2}} +{a}+\mathrm{1}}{\:\:\:\:{a}^{\mathrm{2}} +{a}+\mathrm{1}}=\frac{\:\:\:\:\mathrm{2}{a}^{\mathrm{2}} −\mathrm{2}{a}\left(−\frac{{a}}{{a}+\mathrm{1}}\right)+\left(−\frac{{a}}{{a}+\mathrm{1}}−{a}\right)}{−\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{a}\left(−\frac{{a}}{{a}+\mathrm{1}}\right)+\left(−\frac{{a}}{{a}+\mathrm{1}}−{a}\right)} \\ $$$$\Rightarrow\frac{−{a}^{\mathrm{2}} +{a}+\mathrm{1}}{\:\:\:\:{a}^{\mathrm{2}} +{a}+\mathrm{1}}=\frac{\:\:\:\:\mathrm{2}{a}^{\mathrm{2}} +\frac{\mathrm{2}{a}^{\mathrm{2}} }{{a}+\mathrm{1}}−\frac{{a}^{\mathrm{2}} +\mathrm{2}{a}}{{a}+\mathrm{1}}}{−\mathrm{2}{a}^{\mathrm{2}} −\frac{\mathrm{2}{a}^{\mathrm{2}} }{{a}+\mathrm{1}}−\frac{{a}^{\mathrm{2}} +\mathrm{2}{a}}{{a}+\mathrm{1}}{r}} \\ $$$$\Rightarrow\frac{−{a}^{\mathrm{2}} +{a}+\mathrm{1}}{\:\:\:\:{a}^{\mathrm{2}} +{a}+\mathrm{1}}=\frac{\:\:\:\:\frac{\mathrm{2}{a}^{\mathrm{3}} +\mathrm{3}{a}^{\mathrm{2}} −\mathrm{2}{a}}{{a}+\mathrm{1}}}{\frac{−\mathrm{2}{a}^{\mathrm{3}} −\mathrm{5}{a}^{\mathrm{2}} −\mathrm{2}{a}}{{a}+\mathrm{1}}} \\ $$$$\Rightarrow\frac{−{a}^{\mathrm{2}} +{a}+\mathrm{1}}{\:\:\:\:{a}^{\mathrm{2}} +{a}+\mathrm{1}}=\frac{\:\:\:\:\mathrm{2}{a}^{\mathrm{2}} +\mathrm{3}{a}−\mathrm{2}}{−\mathrm{2}{a}^{\mathrm{2}} −\mathrm{5}{a}−\mathrm{2}} \\ $$$$\Rightarrow\frac{−{a}^{\mathrm{2}} +{a}+\mathrm{1}+{a}^{\mathrm{2}} +{a}+\mathrm{1}}{\:\:\:\:{a}^{\mathrm{2}} +{a}+\mathrm{1}}=\frac{\:\:\:\:\mathrm{2}{a}^{\mathrm{2}} +\mathrm{3}{a}−\mathrm{2}−\mathrm{2}{a}^{\mathrm{2}} −\mathrm{5}{a}−\mathrm{2}}{−\mathrm{2}{a}^{\mathrm{2}} −\mathrm{5}{a}−\mathrm{2}} \\ $$$$\Rightarrow\frac{{a}+\mathrm{1}}{\:\:\:\:{a}^{\mathrm{2}} +{a}+\mathrm{1}}=\frac{\:\:\:\:{a}+\mathrm{2}}{\mathrm{2}{a}^{\mathrm{2}} +\mathrm{5}{a}+\mathrm{2}} \\ $$$$\Rightarrow\frac{{a}+\mathrm{1}}{\:\:\:\:{a}^{\mathrm{2}} +{a}+\mathrm{1}}=\frac{\:\:\:\:{a}+\mathrm{2}}{\left({a}+\mathrm{2}\right)\left(\mathrm{2}{a}+\mathrm{1}\right)} \\ $$$$\Rightarrow\frac{{a}+\mathrm{1}}{\:\:\:\:{a}^{\mathrm{2}} +{a}+\mathrm{1}}=\frac{\:\:\:\:\mathrm{1}}{\mathrm{2}{a}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\mathrm{2}{a}^{\mathrm{2}} +\mathrm{3}{a}+\mathrm{1}−{a}^{\mathrm{2}} −{a}−\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:{a}^{\mathrm{2}} +\mathrm{2}{a}=\mathrm{0} \\ $$$${a}=\mathrm{0}\:\mid\:{a}=−\mathrm{2} \\ $$$${a}=\mathrm{0}\wedge{b}=\mathrm{0}\:\mid\:{a}=−\mathrm{2}\wedge{b}=−\mathrm{2} \\ $$
Answered by ajfour last updated on 14/Sep/19
![Let ratios be equal to k. Value of a, taking a=b doesn′t fulfill the demand where this is required. (a+1−a^2 )=k(a+1+a^2 ) (k+1)a^2 +(k−1)a+(k−1)=0 a, b are roots of the eq. ab=((k−1)/(k+1)) , a+b=−(((k−1))/((k+1))) Also from comparing other two fractions if a≠b, i obtain a+2b+2=0 ⇒ a=−2b−2 −2(b+1)b=((k−1)/(k+1)) & −2(b+1)+b=((1−k)/(1+k)) ⇒ ((b+2)/(b(b+1)))=−2 ⇒ 2b^2 +2b+b+2=0 2b^2 +3b+2=0 b=((−3±(√(9−16)))/4) a= −2[1−(3/4)±((i(√7))/4)] =−(1/2)±((i(√7))/2) if we dont assume a=b.](https://www.tinkutara.com/question/Q68641.png)
$${Let}\:{ratios}\:{be}\:{equal}\:{to}\:{k}.\:{Value}\:{of} \\ $$$$\:\boldsymbol{{a}},\:{taking}\:{a}={b}\:{doesn}'{t}\:{fulfill} \\ $$$${the}\:{demand}\:{where}\:{this}\:{is} \\ $$$${required}. \\ $$$$\left({a}+\mathrm{1}−{a}^{\mathrm{2}} \right)={k}\left({a}+\mathrm{1}+{a}^{\mathrm{2}} \right) \\ $$$$\left({k}+\mathrm{1}\right){a}^{\mathrm{2}} +\left({k}−\mathrm{1}\right){a}+\left({k}−\mathrm{1}\right)=\mathrm{0} \\ $$$${a},\:{b}\:{are}\:{roots}\:{of}\:{the}\:{eq}. \\ $$$${ab}=\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}}\:,\:\:{a}+{b}=−\frac{\left({k}−\mathrm{1}\right)}{\left({k}+\mathrm{1}\right)} \\ $$$${Also} \\ $$$$\:{from}\:{comparing}\:{other}\:{two} \\ $$$${fractions}\:{if}\:{a}\neq{b},\:{i}\:{obtain} \\ $$$$\:{a}+\mathrm{2}{b}+\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\:{a}=−\mathrm{2}{b}−\mathrm{2} \\ $$$$\:−\mathrm{2}\left({b}+\mathrm{1}\right){b}=\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}} \\ $$$$\&\:\:\:\:−\mathrm{2}\left({b}+\mathrm{1}\right)+{b}=\frac{\mathrm{1}−{k}}{\mathrm{1}+{k}} \\ $$$$\Rightarrow\:\:\:\frac{{b}+\mathrm{2}}{{b}\left({b}+\mathrm{1}\right)}=−\mathrm{2} \\ $$$$\Rightarrow\:\:\:\mathrm{2}{b}^{\mathrm{2}} +\mathrm{2}{b}+{b}+\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{2}{b}^{\mathrm{2}} +\mathrm{3}{b}+\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:{b}=\frac{−\mathrm{3}\pm\sqrt{\mathrm{9}−\mathrm{16}}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:{a}=\:−\mathrm{2}\left[\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}\pm\frac{{i}\sqrt{\mathrm{7}}}{\mathrm{4}}\right] \\ $$$$\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{{i}\sqrt{\mathrm{7}}}{\mathrm{2}}\:\:\:\:{if}\:{we}\:{dont} \\ $$$${assume}\:{a}={b}. \\ $$
