Question Number 134182 by Algoritm last updated on 28/Feb/21
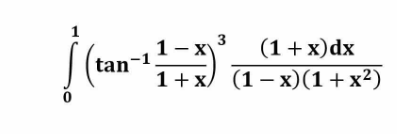
Answered by Ñï= last updated on 01/Mar/21
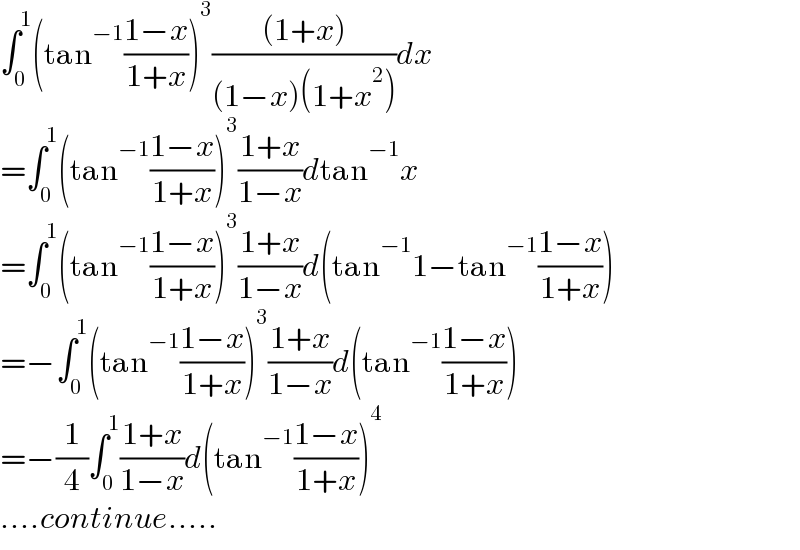
$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)^{\mathrm{3}} \frac{\left(\mathrm{1}+{x}\right)}{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)^{\mathrm{3}} \frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}{d}\mathrm{tan}^{−\mathrm{1}} {x} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)^{\mathrm{3}} \frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}{d}\left(\mathrm{tan}^{−\mathrm{1}} \mathrm{1}−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right) \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)^{\mathrm{3}} \frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}{d}\left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}{d}\left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)^{\mathrm{4}} \\ $$$$….{continue}….. \\ $$
