Question Number 3113 by Yozzi last updated on 05/Dec/15
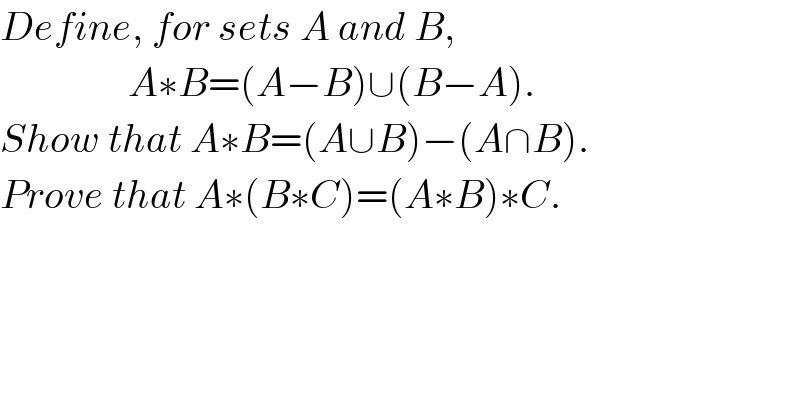
$${Define},\:{for}\:{sets}\:{A}\:{and}\:{B}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{A}\ast{B}=\left({A}−{B}\right)\cup\left({B}−{A}\right). \\ $$$${Show}\:{that}\:{A}\ast{B}=\left({A}\cup{B}\right)−\left({A}\cap{B}\right). \\ $$$${Prove}\:{that}\:{A}\ast\left({B}\ast{C}\right)=\left({A}\ast{B}\right)\ast{C}.\: \\ $$
Commented by Yozzi last updated on 06/Dec/15

$${It}\:{is}\:{proof}\:{of}\:{the}\:{associativity}\:{of}\:{the} \\ $$$${operation}\:\ast\:{which}\:{is}\:{giving}\:{me}\: \\ $$$${trouble}.\:{My}\:{current}\:{mental}\:{approach}\: \\ $$$${includes}\:{a}\:{consideration}\:{of}\:{a}\: \\ $$$${general}\:{Venn}\:{diagram}\:{for}\:\mathrm{3}\:{sets}, \\ $$$${after}\:{making}\:{an}\:{unsucessful}\:{algebraic}\:{attempt}. \\ $$$$\left({Hopefully}\:{I}'{ll}\:{determine}\:{an}\:\right. \\ $$$$\left.{algebraic}\:{solution},{soon}…\right) \\ $$
Commented by prakash jain last updated on 06/Dec/15
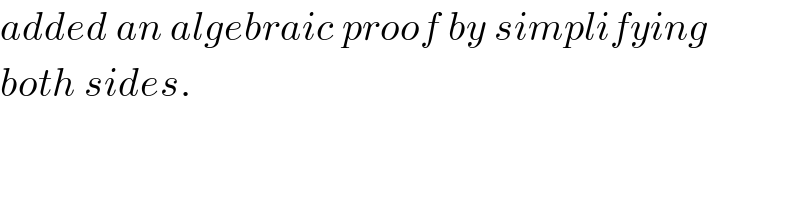
$${added}\:{an}\:{algebraic}\:{proof}\:{by}\:{simplifying} \\ $$$${both}\:{sides}. \\ $$
Commented by Yozzi last updated on 06/Dec/15
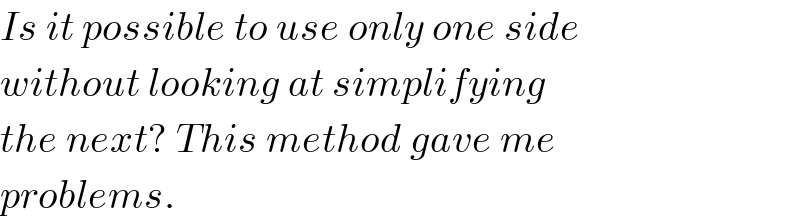
$${Is}\:{it}\:{possible}\:{to}\:{use}\:{only}\:{one}\:{side} \\ $$$${without}\:{looking}\:{at}\:{simplifying} \\ $$$${the}\:{next}?\:{This}\:{method}\:{gave}\:{me} \\ $$$${problems}.\: \\ $$
Commented by prakash jain last updated on 06/Dec/15

$$\mathrm{Given}\:\mathrm{the}\:\mathrm{proof}\:\mathrm{start}\:\mathrm{at}\:\mathrm{the}\:\mathrm{last}\:\mathrm{step}\:\mathrm{of} \\ $$$$\mathrm{LHS}\:\mathrm{and}\:\mathrm{do}\:\mathrm{RHS}\:\mathrm{steps}\:\mathrm{in}\:\mathrm{reverse}\:\mathrm{order}! \\ $$
Answered by prakash jain last updated on 05/Dec/15
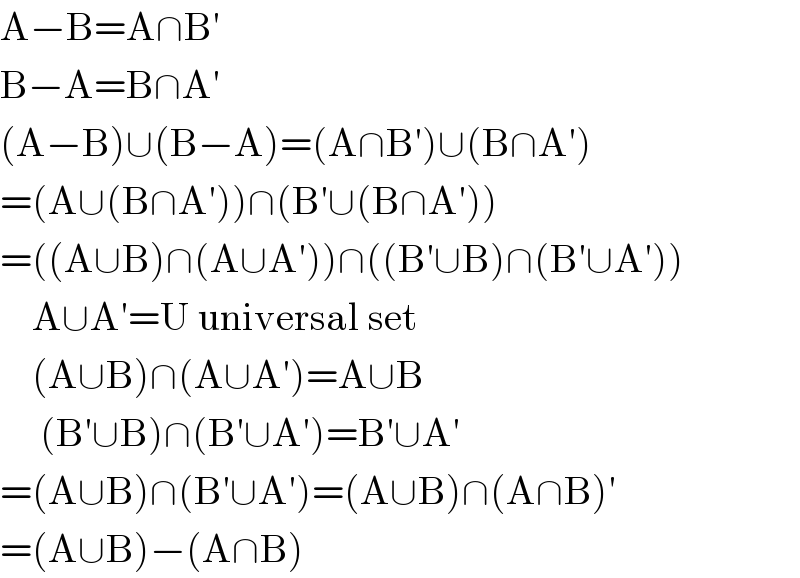
$$\mathrm{A}−\mathrm{B}=\mathrm{A}\cap\mathrm{B}' \\ $$$$\mathrm{B}−\mathrm{A}=\mathrm{B}\cap\mathrm{A}' \\ $$$$\left(\mathrm{A}−\mathrm{B}\right)\cup\left(\mathrm{B}−\mathrm{A}\right)=\left(\mathrm{A}\cap\mathrm{B}'\right)\cup\left(\mathrm{B}\cap\mathrm{A}'\right) \\ $$$$=\left(\mathrm{A}\cup\left(\mathrm{B}\cap\mathrm{A}'\right)\right)\cap\left(\mathrm{B}'\cup\left(\mathrm{B}\cap\mathrm{A}'\right)\right) \\ $$$$=\left(\left(\mathrm{A}\cup\mathrm{B}\right)\cap\left(\mathrm{A}\cup\mathrm{A}'\right)\right)\cap\left(\left(\mathrm{B}'\cup\mathrm{B}\right)\cap\left(\mathrm{B}'\cup\mathrm{A}'\right)\right) \\ $$$$\:\:\:\:\mathrm{A}\cup\mathrm{A}'=\mathrm{U}\:\mathrm{universal}\:\mathrm{set} \\ $$$$\:\:\:\:\left(\mathrm{A}\cup\mathrm{B}\right)\cap\left(\mathrm{A}\cup\mathrm{A}'\right)=\mathrm{A}\cup\mathrm{B} \\ $$$$\:\:\:\:\:\left(\mathrm{B}'\cup\mathrm{B}\right)\cap\left(\mathrm{B}'\cup\mathrm{A}'\right)=\mathrm{B}'\cup\mathrm{A}' \\ $$$$=\left(\mathrm{A}\cup\mathrm{B}\right)\cap\left(\mathrm{B}'\cup\mathrm{A}'\right)=\left(\mathrm{A}\cup\mathrm{B}\right)\cap\left(\mathrm{A}\cap\mathrm{B}\right)' \\ $$$$=\left(\mathrm{A}\cup\mathrm{B}\right)−\left(\mathrm{A}\cap\mathrm{B}\right) \\ $$
Commented by Rasheed Soomro last updated on 06/Dec/15

$$\:\:\:\:\:\:\:\:\:\:\mathcal{G}^{\overset{\mathcal{V}} {\mathcal{OO}}} \mathcal{D}\:\:\:\:! \\ $$
Answered by prakash jain last updated on 06/Dec/15

$$\mathrm{RHS}=\left(\mathrm{A}\ast\mathrm{B}\right)\ast\mathrm{C} \\ $$$$=\left(\left(\mathrm{A}\cap\mathrm{B}'\right)\cup\left(\mathrm{A}'\cap\mathrm{B}\right)\right)\ast\mathrm{C} \\ $$$$=\left(\left(\left(\mathrm{A}\cap\mathrm{B}'\right)\cup\left(\mathrm{A}'\cap\mathrm{B}\right)\right)\cap\mathrm{C}'\right)\cup\left(\left(\left(\mathrm{A}\cap\mathrm{B}'\right)\cup\left(\mathrm{A}'\cap\mathrm{B}\right)\right)'\cap\mathrm{C}\right) \\ $$$$\:\:\:\:\:\:\:\:\left(\mathrm{A}\cap\mathrm{B}'\right)\cup\left(\mathrm{A}'\cap\mathrm{B}\right)=\left(\mathrm{A}\cup\mathrm{B}\right)\cap\left(\mathrm{A}\cap\mathrm{B}\right)'\:\mathrm{see}\:\mathrm{proof}\:\mathrm{in}\:\mathrm{prev}\:\mathrm{ans} \\ $$$$=\left(\left(\mathrm{A}\cap\mathrm{B}'\cap\mathrm{C}'\right)\cup\left(\mathrm{A}'\cap\mathrm{B}\cap\mathrm{C}'\right)\right)\cup\left(\left(\left(\mathrm{A}\cup\mathrm{B}\right)\cap\left(\mathrm{A}\cap\mathrm{B}\right)'\right)'\cap\mathrm{C}\right) \\ $$$$=\left(\left(\mathrm{A}\cap\mathrm{B}'\cap\mathrm{C}'\right)\cup\left(\mathrm{A}'\cap\mathrm{B}\cap\mathrm{C}'\right)\right)\cup\left(\left(\left(\mathrm{A}\cup\mathrm{B}\right)'\cup\left(\mathrm{A}\cap\mathrm{B}\right)\right)\cap\mathrm{C}\right) \\ $$$$=\left(\left(\mathrm{A}\cap\mathrm{B}'\cap\mathrm{C}'\right)\cup\left(\mathrm{A}'\cap\mathrm{B}\cap\mathrm{C}'\right)\right)\cup\left(\left(\left(\mathrm{A}'\cap\mathrm{B}'\right)\cup\left(\mathrm{A}\cap\mathrm{B}\right)\right)\cap\mathrm{C}\right) \\ $$$$=\left(\left(\mathrm{A}\cap\mathrm{B}'\cap\mathrm{C}'\right)\cup\left(\mathrm{A}'\cap\mathrm{B}\cap\mathrm{C}'\right)\right)\cup\left(\left(\mathrm{A}'\cap\mathrm{B}'\cap\mathrm{C}\right)\cup\left(\mathrm{A}\cap\mathrm{B}\cap\mathrm{C}\right)\right) \\ $$$$=\left(\mathrm{A}\cap\mathrm{B}'\cap\mathrm{C}'\right)\cup\left(\mathrm{A}'\cap\mathrm{B}\cap\mathrm{C}'\right)\cup\left(\mathrm{A}'\cap\mathrm{B}'\cap\mathrm{C}\right)\cup\left(\mathrm{A}\cap\mathrm{B}\cap\mathrm{C}\right) \\ $$$$\mathrm{LHS}=\mathrm{A}\ast\left(\mathrm{B}\ast\mathrm{C}\right) \\ $$$$=\left(\mathrm{A}\cap\left(\left(\mathrm{B}\cap\mathrm{C}'\right)\cup\left(\mathrm{B}'\cap\mathrm{C}\right)\right)'\right)\cup\left(\mathrm{A}'\cap\left(\left(\mathrm{B}\cap\mathrm{C}'\right)\cup\left(\mathrm{B}'\cap\mathrm{C}\right)\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\left(\mathrm{B}\cap\mathrm{C}'\right)\cup\left(\mathrm{B}'\cap\mathrm{C}\right)=\left(\mathrm{B}\cup\mathrm{C}\right)\cap\left(\mathrm{B}\cap\mathrm{C}\right)'\:\mathrm{see}\:\mathrm{proof}\:\mathrm{in}\:\mathrm{prev}\:\mathrm{ans} \\ $$$$=\left(\mathrm{A}\cap\left(\left(\mathrm{B}\cup\mathrm{C}\right)\cap\left(\mathrm{B}\cap\mathrm{C}\right)'\right)'\right)\cup\left(\left(\mathrm{A}'\cap\mathrm{B}\cap\mathrm{C}'\right)\cup\left(\mathrm{A}'\cap\mathrm{B}'\cap\mathrm{C}\right)\right) \\ $$$$=\left(\mathrm{A}\cap\left(\left(\mathrm{B}\cup\mathrm{C}\right)'\cup\left(\mathrm{B}\cap\mathrm{C}\right)\right)\right)\cup\left(\left(\mathrm{A}'\cap\mathrm{B}\cap\mathrm{C}'\right)\cup\left(\mathrm{A}'\cap\mathrm{B}'\cap\mathrm{C}\right)\right) \\ $$$$=\left(\mathrm{A}\cap\left(\left(\mathrm{B}'\cap\mathrm{C}'\right)\cup\left(\mathrm{B}\cap\mathrm{C}\right)\right)\right)\cup\left(\left(\mathrm{A}'\cap\mathrm{B}\cap\mathrm{C}'\right)\cup\left(\mathrm{A}'\cap\mathrm{B}'\cap\mathrm{C}\right)\right) \\ $$$$=\left(\mathrm{A}\cap\mathrm{B}'\cap\mathrm{C}'\right)\cup\left(\mathrm{A}\cap\mathrm{B}\cap\mathrm{C}\right)\cup\left(\mathrm{A}'\cap\mathrm{B}\cap\mathrm{C}'\right)\cup\left(\mathrm{A}'\cap\mathrm{B}'\cap\mathrm{C}\right) \\ $$$$\mathrm{LHS}=\mathrm{RHS} \\ $$
