Question Number 134185 by mnjuly1970 last updated on 28/Feb/21
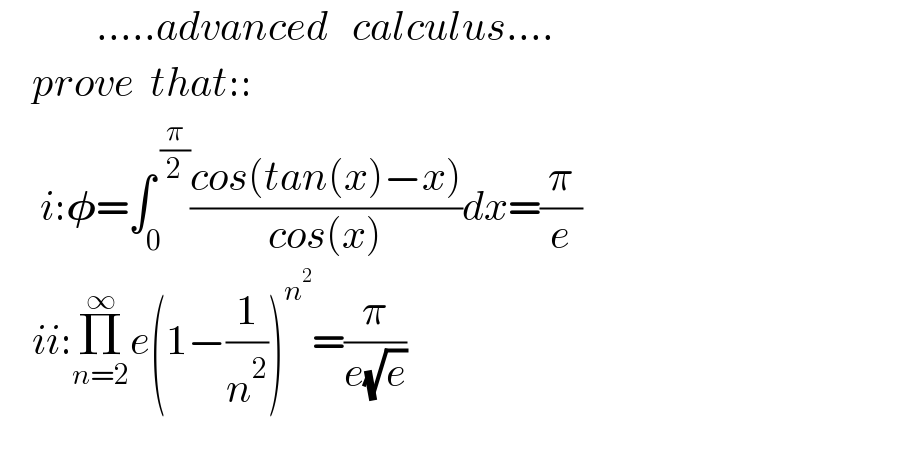
$$\:\:\:\:\:\:\:\:\:\:\:\:…..{advanced}\:\:\:{calculus}…. \\ $$$$\:\:\:\:{prove}\:\:{that}:: \\ $$$$\:\:\:\:\:{i}:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{{cos}\left({tan}\left({x}\right)−{x}\right)}{{cos}\left({x}\right)}{dx}=\frac{\pi}{{e}} \\ $$$$\:\:\:\:{ii}:\underset{{n}=\mathrm{2}} {\overset{\infty} {\prod}}{e}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)^{{n}^{\mathrm{2}} } =\frac{\pi}{{e}\sqrt{{e}}} \\ $$$$\:\: \\ $$
Answered by mindispower last updated on 28/Feb/21
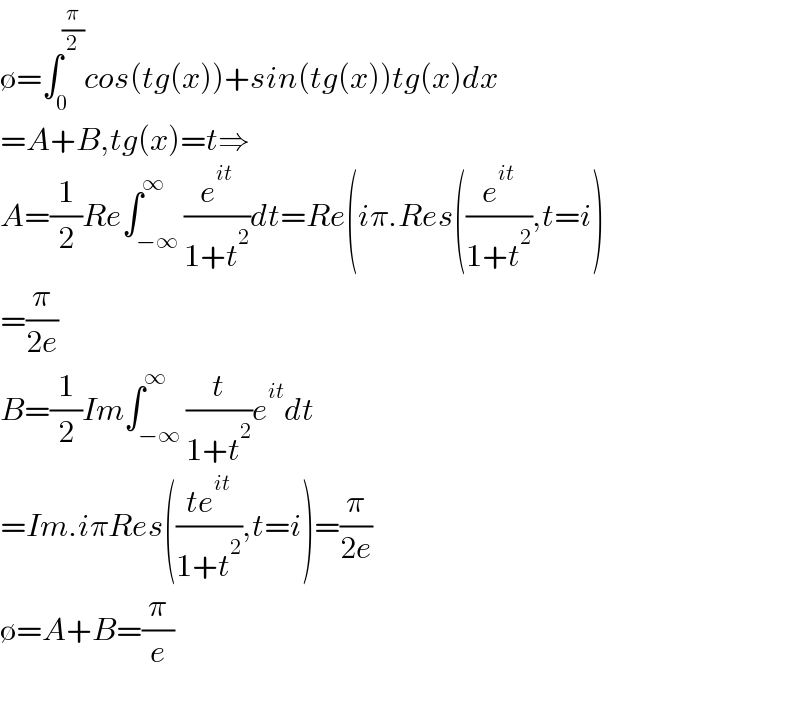
$$\emptyset=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left({tg}\left({x}\right)\right)+{sin}\left({tg}\left({x}\right)\right){tg}\left({x}\right){dx} \\ $$$$={A}+{B},{tg}\left({x}\right)={t}\Rightarrow \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}{Re}\int_{−\infty} ^{\infty} \frac{{e}^{{it}} }{\mathrm{1}+{t}^{\mathrm{2}} }{dt}={Re}\left({i}\pi.{Res}\left(\frac{{e}^{{it}} }{\mathrm{1}+{t}^{\mathrm{2}} },{t}={i}\right)\right. \\ $$$$=\frac{\pi}{\mathrm{2}{e}} \\ $$$${B}=\frac{\mathrm{1}}{\mathrm{2}}{Im}\int_{−\infty} ^{\infty} \frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }{e}^{{it}} {dt} \\ $$$$={Im}.{i}\pi{Res}\left(\frac{{te}^{{it}} }{\mathrm{1}+{t}^{\mathrm{2}} },{t}={i}\right)=\frac{\pi}{\mathrm{2}{e}} \\ $$$$\emptyset={A}+{B}=\frac{\pi}{{e}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 28/Feb/21
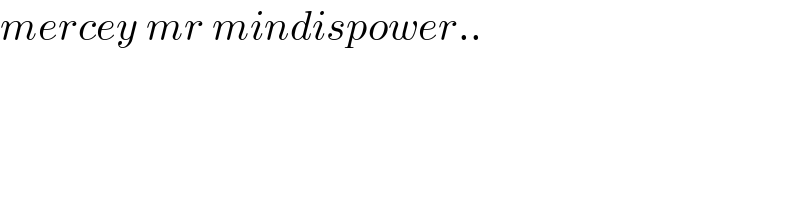
$${mercey}\:{mr}\:{mindispower}.. \\ $$
