Menu Close

A-2-0-1-2-h-and-k-are-numbers-so-that-A-2-hA-kI-where-I-1-0-0-1-find-the-value-of-h-and-k-

Tinku Tara 0 Comments
Pin




Question Number 32869 by Rio Mike last updated on 04/Apr/18
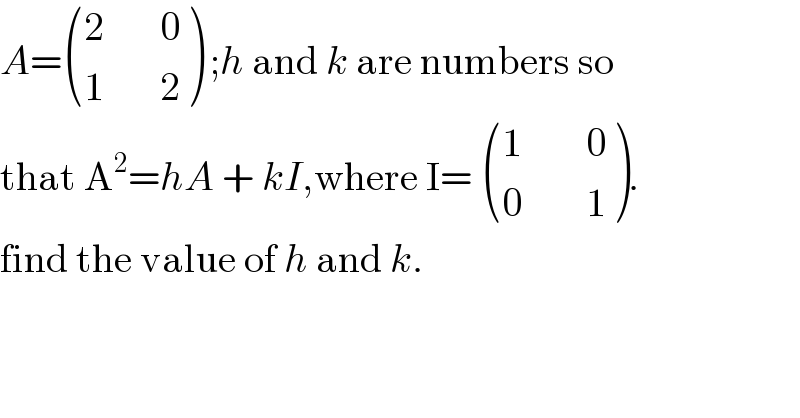
A= (((2 0)),((1 2)) ) ;h and k are numbers so that A^2 =hA + kI,where I= (((1 0)),((0 1)) ). find the value of h and k.
$${A}=\begin{pmatrix}{\mathrm{2}\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{1}\:\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}\:;{h}\:\mathrm{and}\:{k}\:\mathrm{are}\:\mathrm{numbers}\:\mathrm{so} \\ $$$$\mathrm{that}\:\mathrm{A}^{\mathrm{2}} ={hA}\:+\:{kI},\mathrm{where}\:\mathrm{I}=\:\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}. \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{h}\:\mathrm{and}\:{k}. \\ $$
Commented by abdo mathsup last updated on 09/Apr/18
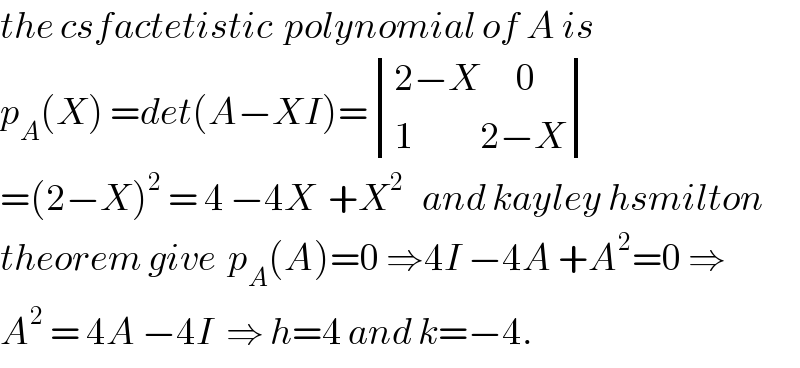
the csfactetistic polynomial of A is p_A (X) =det(A−XI)= determinant (((2−X 0)),((1 2−X))) =(2−X)^2 = 4 −4X +X^2 and kayley hsmilton theorem give p_A (A)=0 ⇒4I −4A +A^2 =0 ⇒ A^2 = 4A −4I ⇒ h=4 and k=−4.
$${the}\:{csfactetistic}\:\:{polynomial}\:{of}\:{A}\:{is} \\ $$$${p}_{{A}} \left({X}\right)\:={det}\left({A}−{XI}\right)=\begin{vmatrix}{\mathrm{2}−{X}\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}−{X}}\end{vmatrix} \\ $$$$=\left(\mathrm{2}−{X}\right)^{\mathrm{2}} \:=\:\mathrm{4}\:−\mathrm{4}{X}\:\:+{X}^{\mathrm{2}} \:\:\:{and}\:{kayley}\:{hsmilton} \\ $$$${theorem}\:{give}\:\:{p}_{{A}} \left({A}\right)=\mathrm{0}\:\Rightarrow\mathrm{4}{I}\:−\mathrm{4}{A}\:+{A}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow \\ $$$${A}^{\mathrm{2}} \:=\:\mathrm{4}{A}\:−\mathrm{4}{I}\:\:\Rightarrow\:{h}=\mathrm{4}\:{and}\:{k}=−\mathrm{4}. \\ $$
Answered by Joel578 last updated on 05/Apr/18
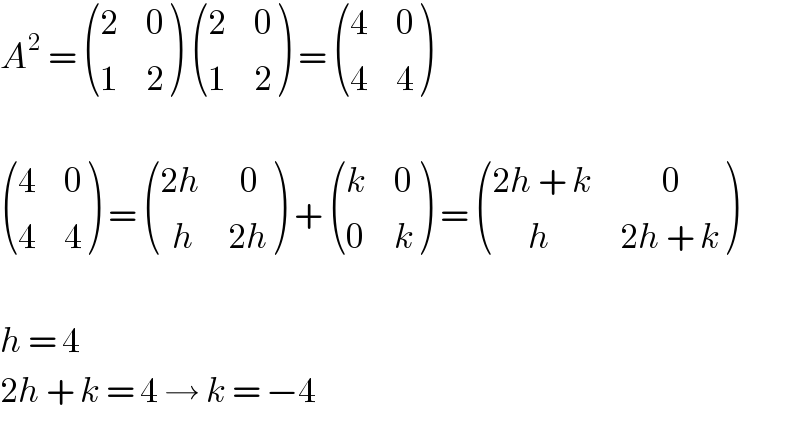
A^2 = ((2,0),(1,2) ) ((2,0),(1,2) ) = ((4,0),(4,4) ) ((4,0),(4,4) ) = (((2h),( 0)),(( h),(2h)) ) + ((k,0),(0,k) ) = (((2h + k),( 0)),(( h),(2h + k)) ) h = 4 2h + k = 4 → k = −4
$${A}^{\mathrm{2}} \:=\:\begin{pmatrix}{\mathrm{2}}&{\mathrm{0}}\\{\mathrm{1}}&{\mathrm{2}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{2}}&{\mathrm{0}}\\{\mathrm{1}}&{\mathrm{2}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{4}}&{\mathrm{0}}\\{\mathrm{4}}&{\mathrm{4}}\end{pmatrix} \\ $$$$ \\ $$$$\begin{pmatrix}{\mathrm{4}}&{\mathrm{0}}\\{\mathrm{4}}&{\mathrm{4}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{2}{h}}&{\:\:\mathrm{0}}\\{\:\:{h}}&{\mathrm{2}{h}}\end{pmatrix}\:+\:\begin{pmatrix}{{k}}&{\mathrm{0}}\\{\mathrm{0}}&{{k}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{2}{h}\:+\:{k}}&{\:\:\:\:\:\:\:\mathrm{0}}\\{\:\:\:\:\:\:{h}}&{\mathrm{2}{h}\:+\:{k}}\end{pmatrix} \\ $$$$ \\ $$$${h}\:=\:\mathrm{4} \\ $$$$\mathrm{2}{h}\:+\:{k}\:=\:\mathrm{4}\:\rightarrow\:{k}\:=\:−\mathrm{4} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *