Question Number 32977 by Mr eaay last updated on 08/Apr/18
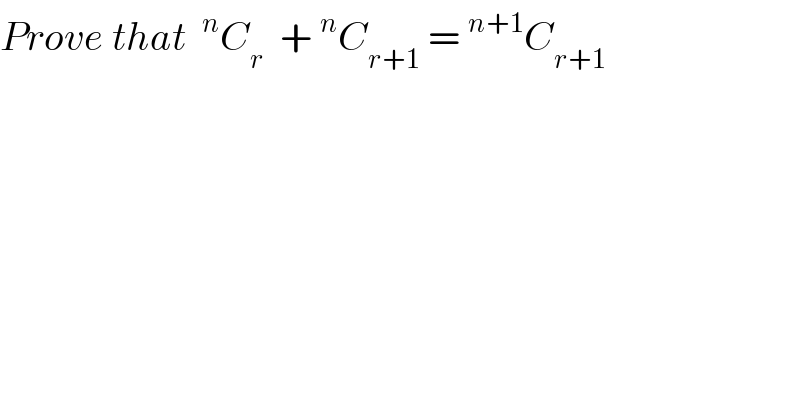
$${Prove}\:{that}\:\:^{{n}} {C}_{{r}} \:\:+\:^{{n}} {C}_{{r}+\mathrm{1}} \:=\:^{{n}+\mathrm{1}} {C}_{{r}+\mathrm{1}} \\ $$$$ \\ $$
Answered by math1967 last updated on 08/Apr/18
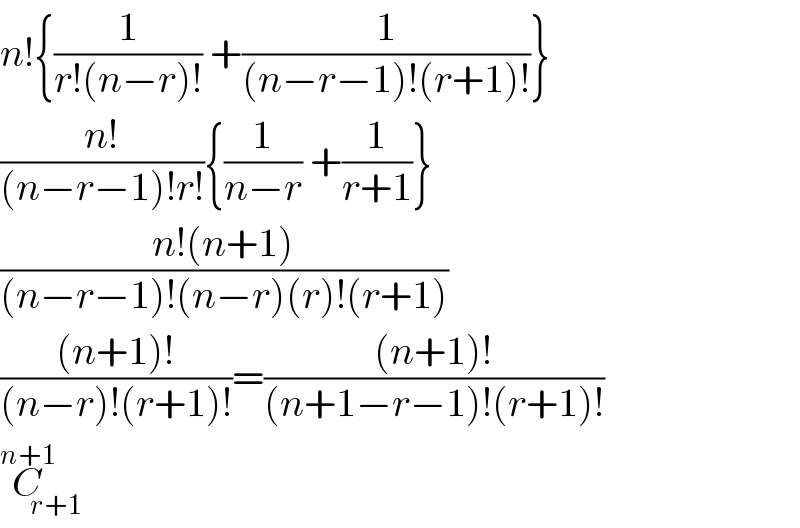
$${n}!\left\{\frac{\mathrm{1}}{{r}!\left({n}−{r}\right)!}\:+\frac{\mathrm{1}}{\left({n}−{r}−\mathrm{1}\right)!\left({r}+\mathrm{1}\right)!}\right\} \\ $$$$\frac{{n}!}{\left({n}−{r}−\mathrm{1}\right)!{r}!}\left\{\frac{\mathrm{1}}{{n}−{r}}\:+\frac{\mathrm{1}}{{r}+\mathrm{1}}\right\} \\ $$$$\frac{{n}!\left({n}+\mathrm{1}\right)}{\left({n}−{r}−\mathrm{1}\right)!\left({n}−{r}\right)\left({r}\right)!\left({r}+\mathrm{1}\right)} \\ $$$$\frac{\left({n}+\mathrm{1}\right)!}{\left({n}−{r}\right)!\left({r}+\mathrm{1}\right)!}=\frac{\left({n}+\mathrm{1}\right)!}{\left({n}+\mathrm{1}−{r}−\mathrm{1}\right)!\left({r}+\mathrm{1}\right)!} \\ $$$$\overset{{n}+\mathrm{1}} {{C}}_{{r}+\mathrm{1}} \\ $$
