Question Number 164138 by LEKOUMA last updated on 14/Jan/22

Answered by floor(10²Eta[1]) last updated on 14/Jan/22
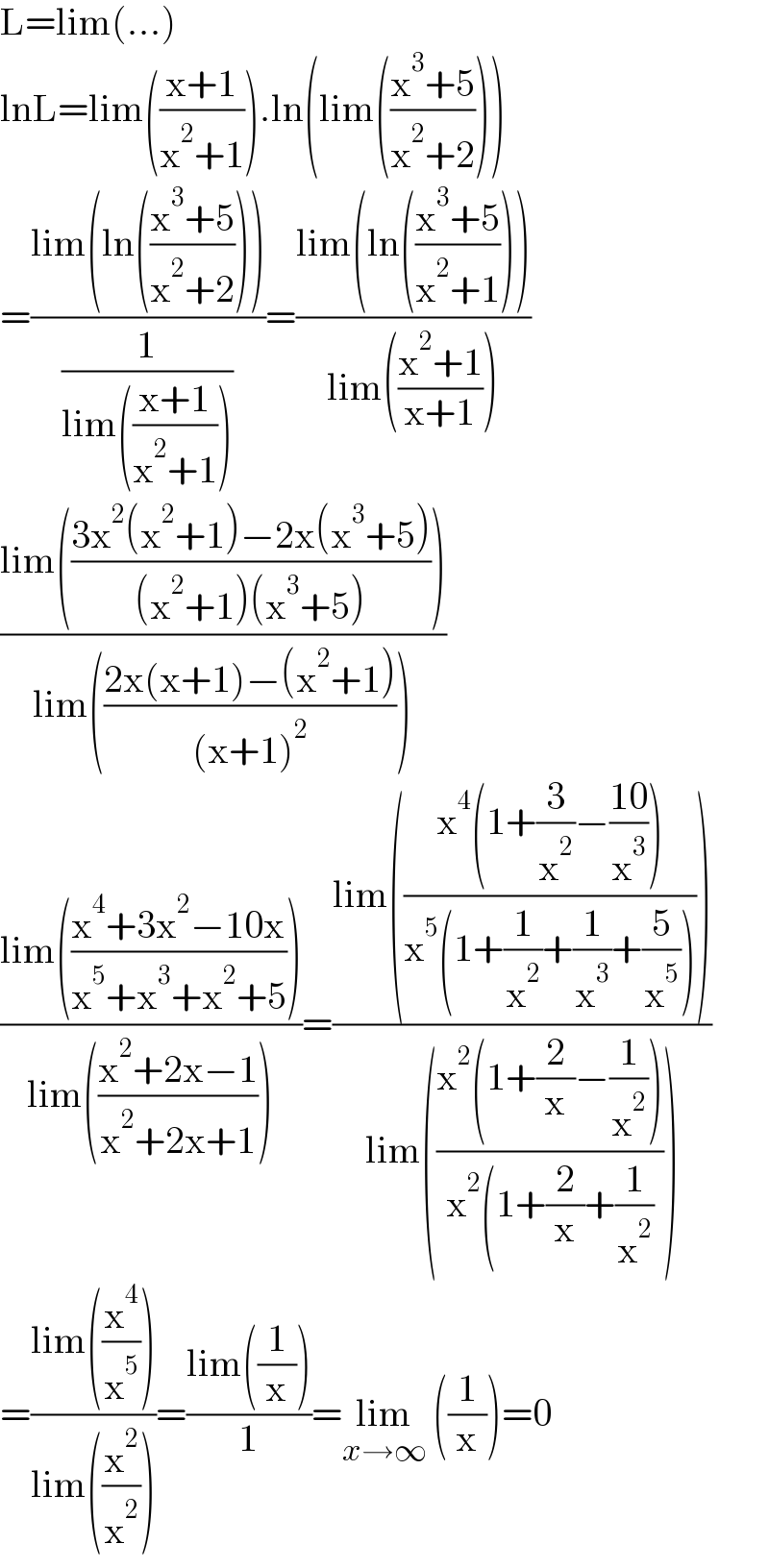
$$\mathrm{L}=\mathrm{lim}\left(…\right) \\ $$$$\mathrm{lnL}=\mathrm{lim}\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right).\mathrm{ln}\left(\mathrm{lim}\left(\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{5}}{\mathrm{x}^{\mathrm{2}} +\mathrm{2}}\right)\right) \\ $$$$=\frac{\mathrm{lim}\left(\mathrm{ln}\left(\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{5}}{\mathrm{x}^{\mathrm{2}} +\mathrm{2}}\right)\right)}{\frac{\mathrm{1}}{\mathrm{lim}\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)}}=\frac{\mathrm{lim}\left(\mathrm{ln}\left(\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{5}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)\right)}{\mathrm{lim}\left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)} \\ $$$$\frac{\mathrm{lim}\left(\frac{\mathrm{3x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{2x}\left(\mathrm{x}^{\mathrm{3}} +\mathrm{5}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{3}} +\mathrm{5}\right)}\right)}{\mathrm{lim}\left(\frac{\mathrm{2x}\left(\mathrm{x}+\mathrm{1}\right)−\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\right)} \\ $$$$\frac{\mathrm{lim}\left(\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{3x}^{\mathrm{2}} −\mathrm{10x}}{\mathrm{x}^{\mathrm{5}} +\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} +\mathrm{5}}\right)}{\mathrm{lim}\left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}}\right)}=\frac{\mathrm{lim}\left(\frac{\mathrm{x}^{\mathrm{4}} \left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{10}}{\mathrm{x}^{\mathrm{3}} }\right)}{\mathrm{x}^{\mathrm{5}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }+\frac{\mathrm{5}}{\mathrm{x}^{\mathrm{5}} }\right)}\right)}{\mathrm{lim}\left(\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right.}\right)} \\ $$$$=\frac{\mathrm{lim}\left(\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{x}^{\mathrm{5}} }\right)}{\mathrm{lim}\left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\right)}=\frac{\mathrm{lim}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)}{\mathrm{1}}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{0}\: \\ $$
