Question Number 33169 by abdo imad last updated on 11/Apr/18
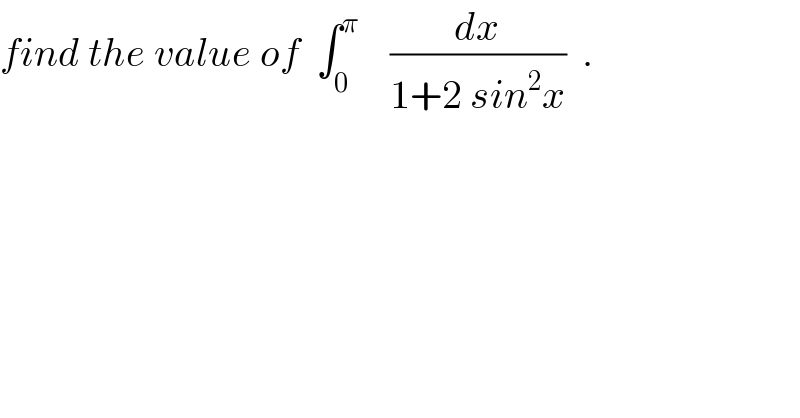
$${find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\frac{{dx}}{\mathrm{1}+\mathrm{2}\:{sin}^{\mathrm{2}} {x}}\:\:. \\ $$
Commented by abdo imad last updated on 12/Apr/18
![let put I =∫_0 ^π (dx/(1+2sin^2 x)) =∫_0 ^π (dx/(1+2(1−cos^2 x))) = ∫_0 ^π (dx/(3 −2cos^2 x)) =∫_0 ^(π/2) (dx/(3 −2 cos^2 x)) + ∫_(π/2) ^π (dx/(3 −2cos^2 x)) =I_1 +I_2 but we knew that 1+tan^2 t =(1/(cos^2 t)) ⇒ cos^2 x = (1/(1+tan^2 x)) ⇒ I_1 = ∫_0 ^(π/2) (dx/(3 −(2/(1+tan^2 x)))) = ∫_0 ^(π/2) ((1+tan^2 x)/(1+3tan^2 x))dx = _(tanx =t) ∫_0 ^(+∞) ((1+t^2 )/(1+3t^2 )) (dt/(1+t^2 )) =∫_0 ^∞ (dt/(1+3t^2 )) =_(t(√3) =u) ∫_0 ^∞ (1/(1+u^2 )) (du/( (√3))) =(1/( (√3))) [arctanu]_0 ^(+∞) I_1 =(π/(2(√3))) let find I_2 ? I_2 = ∫_(π/2) ^π (dx/(3 −2 cos^2 x)) =_(x = π −t) ∫_(π/2) ^0 ((−dt)/(3 −2 cos^2 t)) =∫_0 ^(π/2) (dt/(3−2cos^2 t)) =I_1 =(π/(2(√3))) ⇒ I = (π/(2(√3))) +(π/(2(√3))) = (π/( (√3))) . ★ I =(π/( (√3))) ★](https://www.tinkutara.com/question/Q33180.png)
$${let}\:{put}\:{I}\:\:=\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{dx}}{\mathrm{1}+\mathrm{2}{sin}^{\mathrm{2}} {x}}\:=\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{dx}}{\mathrm{1}+\mathrm{2}\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right)} \\ $$$$=\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\frac{{dx}}{\mathrm{3}\:−\mathrm{2}{cos}^{\mathrm{2}} {x}}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{dx}}{\mathrm{3}\:−\mathrm{2}\:{cos}^{\mathrm{2}} {x}}\:+\:\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:\:\:\frac{{dx}}{\mathrm{3}\:−\mathrm{2}{cos}^{\mathrm{2}} {x}} \\ $$$$={I}_{\mathrm{1}} \:+{I}_{\mathrm{2}} \:\:\:{but}\:{we}\:{knew}\:{that}\:\:\mathrm{1}+{tan}^{\mathrm{2}} {t}\:=\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {t}}\:\Rightarrow \\ $$$${cos}^{\mathrm{2}} {x}\:=\:\frac{\mathrm{1}}{\mathrm{1}+{tan}^{\mathrm{2}} {x}}\:\Rightarrow\:{I}_{\mathrm{1}} =\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\frac{{dx}}{\mathrm{3}\:−\frac{\mathrm{2}}{\mathrm{1}+{tan}^{\mathrm{2}} {x}}} \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{\mathrm{1}+{tan}^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{3}{tan}^{\mathrm{2}} {x}}{dx}\:\:=\:_{{tanx}\:={t}} \:\int_{\mathrm{0}} ^{+\infty} \:\:\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{3}{t}^{\mathrm{2}} }\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{\mathrm{1}+\mathrm{3}{t}^{\mathrm{2}} }\:\:=_{{t}\sqrt{\mathrm{3}}\:={u}} \:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{{du}}{\:\sqrt{\mathrm{3}}}\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\left[{arctanu}\right]_{\mathrm{0}} ^{+\infty} \\ $$$${I}_{\mathrm{1}} \:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:\:{let}\:{find}\:{I}_{\mathrm{2}} ? \\ $$$${I}_{\mathrm{2}} \:=\:\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:\:\frac{{dx}}{\mathrm{3}\:−\mathrm{2}\:{cos}^{\mathrm{2}} {x}}\:\:=_{{x}\:=\:\pi\:−{t}} \:\:\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \:\:\:\frac{−{dt}}{\mathrm{3}\:−\mathrm{2}\:{cos}^{\mathrm{2}} {t}}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dt}}{\mathrm{3}−\mathrm{2}{cos}^{\mathrm{2}} {t}} \\ $$$$={I}_{\mathrm{1}} \:\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:\:\Rightarrow\:\:{I}\:\:=\:\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:=\:\frac{\pi}{\:\sqrt{\mathrm{3}}}\:\:. \\ $$$$\bigstar\:{I}\:=\frac{\pi}{\:\sqrt{\mathrm{3}}}\:\bigstar \\ $$
Answered by sma3l2996 last updated on 11/Apr/18
![I=∫_0 ^π (dx/(1+2sin^2 x)) t=tanx⇒dx=(dt/(1+t^2 )) sin^2 x=(t^2 /(1+t^2 )) I=∫_0 ^∞ (dt/(1+t^2 +2t^2 ))=∫_0 ^∞ (dt/(3t^2 +1)) u=(√3)x⇒dx=((√3)/3)du I=((√3)/3)∫_0 ^∞ (du/(u^2 +1))=((√3)/3)[tan^(−1) (u)]_0 ^∞ I=((√3)/6)π](https://www.tinkutara.com/question/Q33177.png)
$${I}=\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{\mathrm{1}+\mathrm{2}{sin}^{\mathrm{2}} {x}} \\ $$$${t}={tanx}\Rightarrow{dx}=\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${sin}^{\mathrm{2}} {x}=\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${I}=\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}^{\mathrm{2}} }=\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$${u}=\sqrt{\mathrm{3}}{x}\Rightarrow{dx}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}{du} \\ $$$${I}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{{du}}{{u}^{\mathrm{2}} +\mathrm{1}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left[{tan}^{−\mathrm{1}} \left({u}\right)\right]_{\mathrm{0}} ^{\infty} \\ $$$${I}=\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\pi \\ $$
Commented by abdo imad last updated on 12/Apr/18
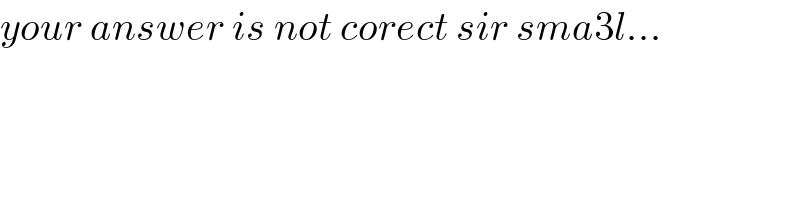
$${your}\:{answer}\:{is}\:{not}\:{corect}\:{sir}\:{sma}\mathrm{3}{l}… \\ $$
