Question Number 164256 by ajfour last updated on 15/Jan/22
Answered by ajfour last updated on 16/Jan/22

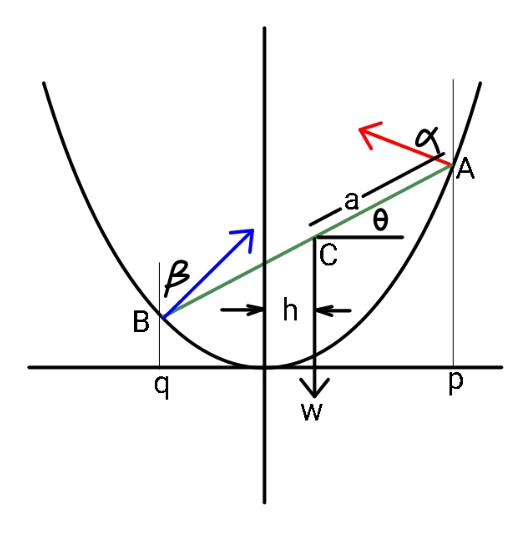
$${A}\:\&\:{B}\:{represent}\:{points}\:{and}\:{also} \\ $$$${forces}\:{at}\:{those}\:{points}\:{respectively}. \\ $$$${q}=−\left(\mathrm{2}{a}\mathrm{cos}\:\theta−{p}\right) \\ $$$$\mathrm{2}{p}=\mathrm{tan}\:\alpha \\ $$$$\mathrm{2}{q}=−\mathrm{tan}\:\beta \\ $$$${Torque}\:{about}\:{B}\: \\ $$$$\left({A}_{{y}} +{B}_{{y}} \right){a}\mathrm{cos}\:\theta={A}_{{y}} \left(\mathrm{2}{a}\mathrm{cos}\:\theta\right)+{A}_{{x}} \left(\mathrm{2}{a}\mathrm{sin}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:….\left({i}\right) \\ $$$${A}_{{x}} ={B}_{{x}} \:\:,\:{A}_{{x}} ={A}_{{y}} \mathrm{tan}\:\alpha=\mathrm{2}{pA}_{{y}} \\ $$$${B}_{{x}} ={B}_{{y}} \mathrm{tan}\:\beta=−\mathrm{2}{qB}_{{y}} \\ $$$$\Rightarrow\:\:\:{A}_{{x}} =\mathrm{2}\left(\mathrm{2}{a}\mathrm{cos}\:\theta−{p}\right){B}_{{y}} \\ $$$$\:\:\:\mathrm{2}{a}\mathrm{sin}\:\theta={p}^{\mathrm{2}} −{q}^{\mathrm{2}} \:\:\Rightarrow \\ $$$${now}\:\frac{\mathrm{2sin}\:\theta}{{a}}=\left(\frac{{p}}{{a}}\right)^{\mathrm{2}} −\left(\mathrm{2cos}\:\theta−\frac{{p}}{{a}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\frac{\mathrm{2sin}\:\theta}{{a}}=\mathrm{4}\left(\frac{{p}}{{a}}\right)\mathrm{cos}\:\theta−\mathrm{4cos}\:^{\mathrm{2}} \theta \\ $$$$\Rightarrow\:\:\:\frac{{p}}{{a}}={t}=\frac{\mathrm{tan}\:\theta}{\mathrm{2}{a}}+\mathrm{cos}\:\theta \\ $$$${from}\:\:….\left({i}\right) \\ $$$$\mathrm{1}+\frac{\mathrm{2}}{\mathrm{2}\left(\mathrm{2cos}\:\theta−\frac{{p}}{{a}}\right)}=\mathrm{2}+\mathrm{4}{p}\mathrm{tan}\:\theta \\ $$$$\Rightarrow\:\:\mathrm{1}+\mathrm{4}{a}\mathrm{tan}\:\theta\left(\frac{\mathrm{tan}\:\theta}{\mathrm{2}{a}}+\mathrm{cos}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{cos}\:\theta−\frac{\mathrm{tan}\:\theta}{\mathrm{2}{a}}} \\ $$$$\Rightarrow\:\:\mathrm{cos}\:\theta−\frac{\mathrm{tan}\:\theta}{\mathrm{2}{a}}+\mathrm{2tan}\:^{\mathrm{2}} \theta\mathrm{cos}\:\theta \\ $$$$\:\:\:−\frac{\mathrm{tan}\:^{\mathrm{2}} \theta}{{a}}+\mathrm{4}{a}\mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2sin}\:\theta\mathrm{tan}\:\theta\:\:\:\:=\:\:\mathrm{1} \\ $$$$\Rightarrow \\ $$$$\mathrm{2}{a}\mathrm{cos}\:^{\mathrm{3}} \theta−\mathrm{sin}\:\theta\mathrm{cos}\:\theta+\mathrm{4}{a}\mathrm{sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:\theta \\ $$$$\:\:\:−\mathrm{2sin}\:^{\mathrm{2}} \theta+\mathrm{8}{a}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:^{\mathrm{3}} \theta \\ $$$$\:\:\:\:\:\:\:\:\:−\mathrm{4}{a}\mathrm{sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:\theta=\mathrm{2}{a}\mathrm{cos}\:^{\mathrm{2}} \theta \\ $$$$ \\ $$
