Question Number 164347 by ajfour last updated on 16/Jan/22
Commented by ajfour last updated on 16/Jan/22

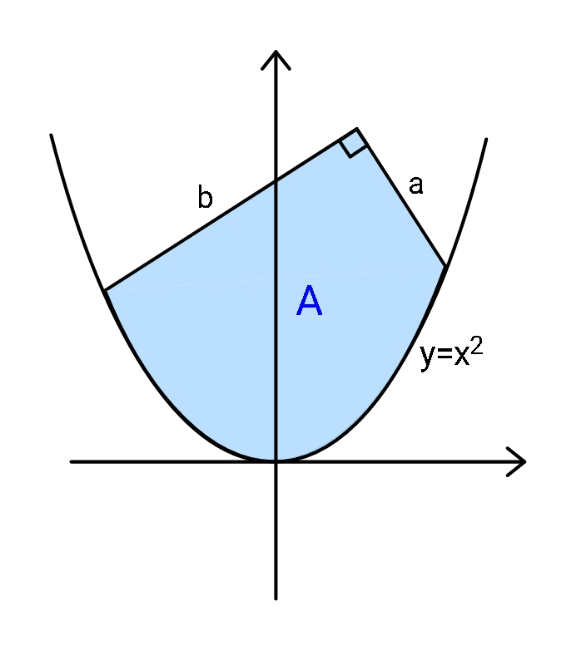
$${Find}\:{maximum}\:{colored}\:{area}\:{A}\left({a},{b}\right). \\ $$
Commented by mr W last updated on 16/Jan/22

Commented by mr W last updated on 16/Jan/22

$${A}={A}_{\mathrm{1}} +{A}_{\mathrm{2}} \\ $$$${A}_{\mathrm{1}} =\frac{{ab}}{\mathrm{2}}\:{is}\:{fixed}. \\ $$$${A}_{{max}} \Leftrightarrow{A}_{\mathrm{2},{max}} \\ $$$${due}\:{to}\:{symmetry},\:{A}_{\mathrm{2},{max}} \:{is}\:{when}\:{c} \\ $$$${is}\:{horizontal}. \\ $$$${c}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${A}_{\mathrm{2},{max}} =\frac{\mathrm{2}}{\mathrm{3}}×{c}×\left(\frac{{c}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{{c}^{\mathrm{3}} }{\mathrm{6}}=\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{6}} \\ $$$$\Rightarrow{A}_{{max}} =\frac{{ab}}{\mathrm{2}}+\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{6}} \\ $$
Commented by ajfour last updated on 16/Jan/22

$${Thanks}\:{sir}. \\ $$
