Question Number 134251 by Dwaipayan Shikari last updated on 01/Mar/21

$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{nsin}\left({n}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 01/Mar/21
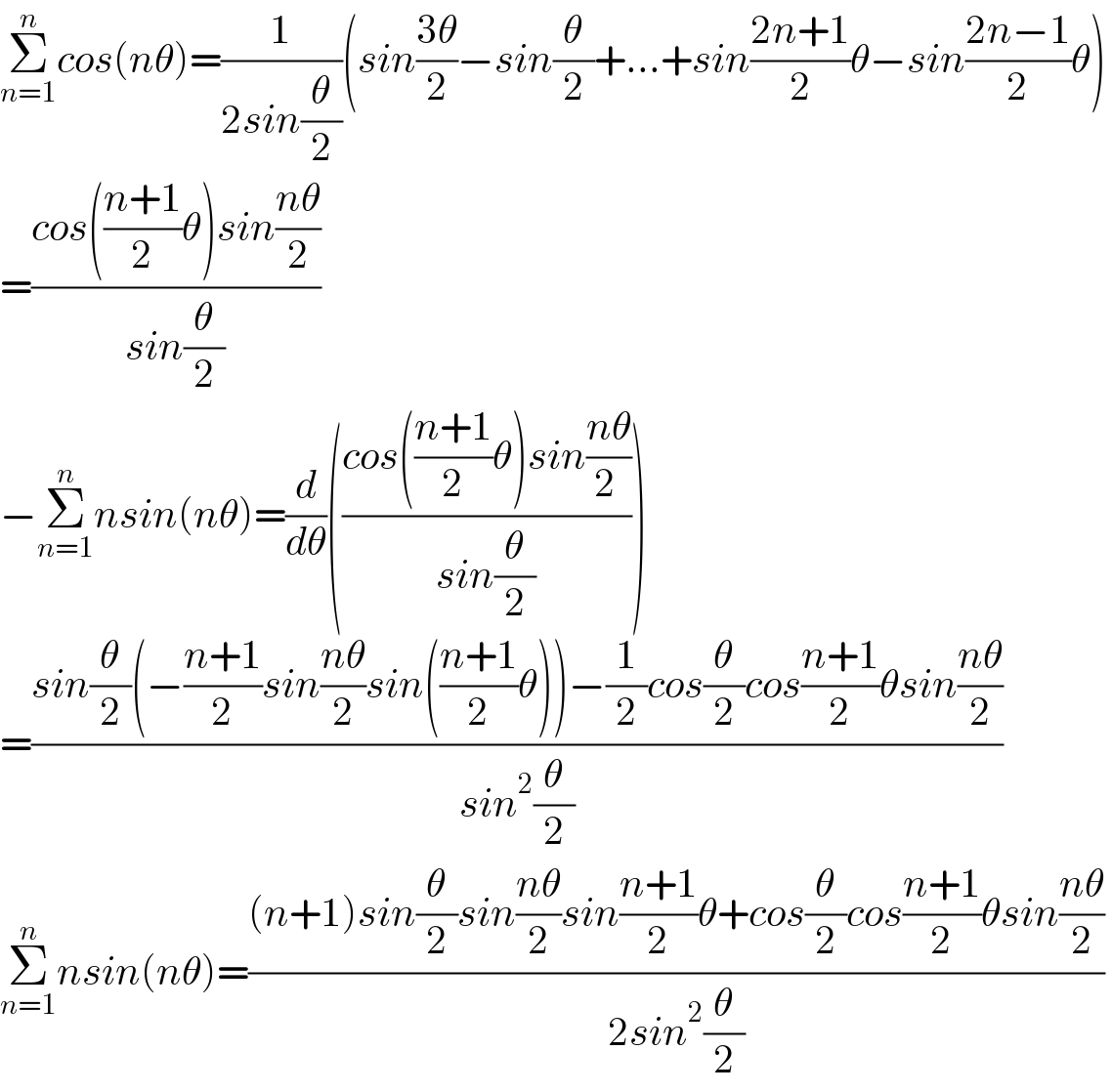
$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{cos}\left({n}\theta\right)=\frac{\mathrm{1}}{\mathrm{2}{sin}\frac{\theta}{\mathrm{2}}}\left({sin}\frac{\mathrm{3}\theta}{\mathrm{2}}−{sin}\frac{\theta}{\mathrm{2}}+…+{sin}\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\theta−{sin}\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}}\theta\right) \\ $$$$=\frac{{cos}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\theta\right){sin}\frac{{n}\theta}{\mathrm{2}}}{{sin}\frac{\theta}{\mathrm{2}}} \\ $$$$−\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{nsin}\left({n}\theta\right)=\frac{{d}}{{d}\theta}\left(\frac{{cos}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\theta\right){sin}\frac{{n}\theta}{\mathrm{2}\:}}{{sin}\frac{\theta}{\mathrm{2}}}\right) \\ $$$$=\frac{{sin}\frac{\theta}{\mathrm{2}}\left(−\frac{{n}+\mathrm{1}}{\mathrm{2}}{sin}\frac{{n}\theta}{\mathrm{2}}{sin}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\theta\right)\right)−\frac{\mathrm{1}}{\mathrm{2}}{cos}\frac{\theta}{\mathrm{2}}{cos}\frac{{n}+\mathrm{1}}{\mathrm{2}}\theta{sin}\frac{{n}\theta}{\mathrm{2}}}{{sin}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}}\: \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{nsin}\left({n}\theta\right)=\frac{\left({n}+\mathrm{1}\right){sin}\frac{\theta}{\mathrm{2}}{sin}\frac{{n}\theta}{\mathrm{2}}{sin}\frac{{n}+\mathrm{1}}{\mathrm{2}}\theta+{cos}\frac{\theta}{\mathrm{2}}{cos}\frac{{n}+\mathrm{1}}{\mathrm{2}}\theta{sin}\frac{{n}\theta}{\mathrm{2}}}{\mathrm{2}{sin}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}}\: \\ $$
