Question Number 134252 by bramlexs22 last updated on 01/Mar/21

$$\:\mathrm{solve}\:\begin{cases}{\mathrm{x}\equiv\:\mathrm{2}\:\left(\mathrm{mod}\:\mathrm{3}\right)}\\{\mathrm{x}\equiv\:\mathrm{5}\:\left(\mathrm{mod}\:\mathrm{7}\right)}\end{cases} \\ $$
Answered by EDWIN88 last updated on 01/Mar/21
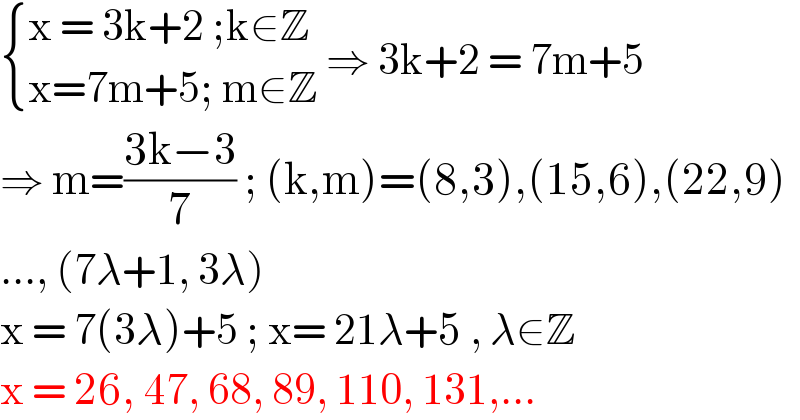
$$\begin{cases}{\mathrm{x}\:=\:\mathrm{3k}+\mathrm{2}\:;\mathrm{k}\in\mathbb{Z}}\\{\mathrm{x}=\mathrm{7m}+\mathrm{5};\:\mathrm{m}\in\mathbb{Z}}\end{cases}\:\Rightarrow\:\mathrm{3k}+\mathrm{2}\:=\:\mathrm{7m}+\mathrm{5} \\ $$$$\Rightarrow\:\mathrm{m}=\frac{\mathrm{3k}−\mathrm{3}}{\mathrm{7}}\:;\:\left(\mathrm{k},\mathrm{m}\right)=\left(\mathrm{8},\mathrm{3}\right),\left(\mathrm{15},\mathrm{6}\right),\left(\mathrm{22},\mathrm{9}\right) \\ $$$$…,\:\left(\mathrm{7}\lambda+\mathrm{1},\:\mathrm{3}\lambda\right) \\ $$$$\mathrm{x}\:=\:\mathrm{7}\left(\mathrm{3}\lambda\right)+\mathrm{5}\:;\:\mathrm{x}=\:\mathrm{21}\lambda+\mathrm{5}\:,\:\lambda\in\mathbb{Z} \\ $$$$\mathrm{x}\:=\:\mathrm{26},\:\mathrm{47},\:\mathrm{68},\:\mathrm{89},\:\mathrm{110},\:\mathrm{131},… \\ $$
