Question Number 134270 by abdurehime last updated on 01/Mar/21
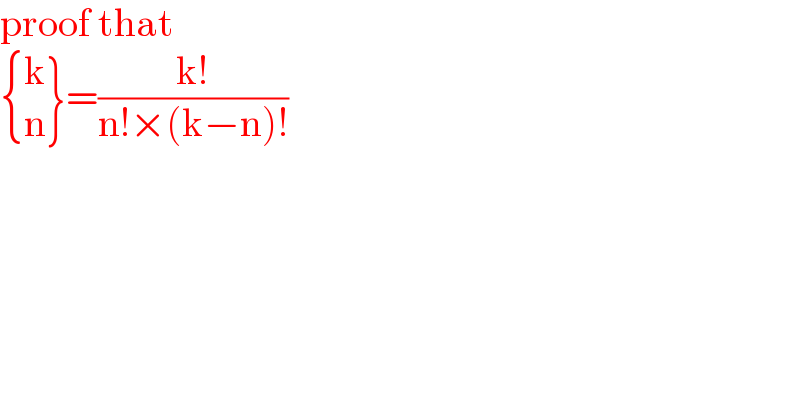
$$\mathrm{proof}\:\mathrm{that} \\ $$$$\left.\begin{cases}{\mathrm{k}}\\{\mathrm{n}}\end{cases}\right\}=\frac{\mathrm{k}!}{\mathrm{n}!×\left(\mathrm{k}−\mathrm{n}\right)!} \\ $$
Commented by mr W last updated on 02/Mar/21
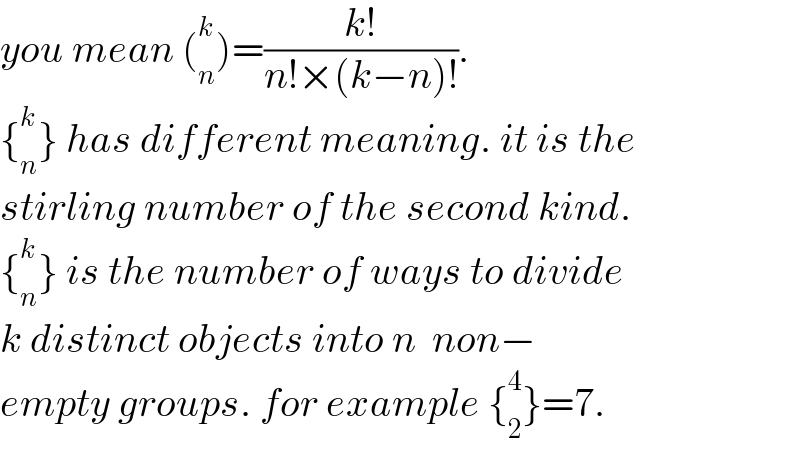
$${you}\:{mean}\:\left(_{{n}} ^{{k}} \right)=\frac{{k}!}{{n}!×\left({k}−{n}\right)!}. \\ $$$$\left\{_{{n}} ^{{k}} \right\}\:{has}\:{different}\:{meaning}.\:{it}\:{is}\:{the} \\ $$$${stirling}\:{number}\:{of}\:{the}\:{second}\:{kind}. \\ $$$$\left\{_{{n}} ^{{k}} \right\}\:{is}\:{the}\:{number}\:{of}\:{ways}\:{to}\:{divide} \\ $$$${k}\:{distinct}\:{objects}\:{into}\:{n}\:\:{non}− \\ $$$${empty}\:{groups}.\:{for}\:{example}\:\left\{_{\mathrm{2}} ^{\mathrm{4}} \right\}=\mathrm{7}. \\ $$
Commented by mr W last updated on 02/Mar/21

$${per}\:{definition}\:\left(_{{n}} ^{{k}} \right)\:{is}\:{the}\:{number}\:{of} \\ $$$${ways}\:{to}\:{choose}\:{n}\:{objects}\:{from}\:{k} \\ $$$${objects}. \\ $$$${to}\:{choose}\:{the}\:{first}\:{object}\:{there}\:{are} \\ $$$${k}\:{ways},\:{to}\:{select}\:{the}\:{second} \\ $$$${object}\:{there}\:{are}\:\left({k}−\mathrm{1}\right)\:{ways}.\:{etc}.\:{to} \\ $$$${select}\:{the}\:{n}−{th}\:{object},\:{there}\:{are} \\ $$$$\left({k}−{n}+\mathrm{1}\right)\:{ways}.\:{totally}\:{there}\:{are} \\ $$$${k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)…\left({k}−{n}+\mathrm{1}\right)\:{ways}.\:{since} \\ $$$${the}\:{order}\:{of}\:{the}\:{n}\:{objects}\:{is}\:{not}\:{of} \\ $$$${concern}, \\ $$$$\left\{_{{n}} ^{{k}} \right\}=\frac{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)…\left({k}−{n}+\mathrm{1}\right)}{{n}!} \\ $$$${this}\:{can}\:{be}\:{simplified}\:{to} \\ $$$$\left\{_{{n}} ^{{k}} \right\}=\frac{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)…\left({k}−{n}+\mathrm{1}\right)\left({k}−{n}\right)\left({k}−{n}−\mathrm{1}\right)…\mathrm{1}}{{n}!\left({k}−{n}\right)\left({k}−{n}−\mathrm{1}\right)…\mathrm{1}} \\ $$$$=\frac{{k}!}{{n}!×\left({k}−{n}\right)!} \\ $$
