Menu Close

let-a-b-c-be-positive-real-numbers-such-that-ab-bc-ac-3-prove-the-inquality-a-b-2-c-2-a-2-bc-b-c-2-a-2-b-2-ac-c-b-2-a-2-c-2-ab-3-

Tinku Tara 0 Comments
Pin




Question Number 98983 by  M±th+et+s last updated on 17/Jun/20
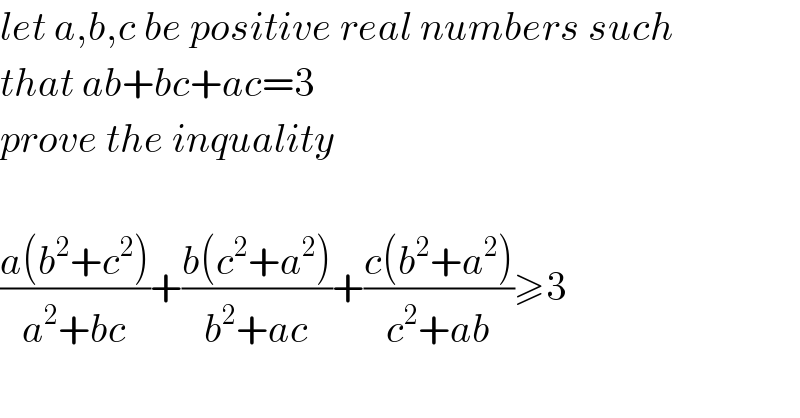
let a,b,c be positive real numbers such that ab+bc+ac=3 prove the inquality ((a(b^2 +c^2 ))/(a^2 +bc))+((b(c^2 +a^2 ))/(b^2 +ac))+((c(b^2 +a^2 ))/(c^2 +ab))≥3
$${let}\:{a},{b},{c}\:{be}\:{positive}\:{real}\:{numbers}\:{such} \\ $$$${that}\:{ab}+{bc}+{ac}=\mathrm{3}\: \\ $$$${prove}\:{the}\:{inquality} \\ $$$$ \\ $$$$\frac{{a}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)}{{a}^{\mathrm{2}} +{bc}}+\frac{{b}\left({c}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} +{ac}}+\frac{{c}\left({b}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)}{{c}^{\mathrm{2}} +{ab}}\geqslant\mathrm{3} \\ $$
Commented by MJS last updated on 17/Jun/20
due to symmetry extremes at a=b=c ⇒ ab+bc+ac=3 ⇔ 3a^2 =3 ⇒ a=±1 but a>0 ⇒ a=b=c=1 the inequation with a=b=c turns into 3a≥3 ⇒ true for a=1 now test if this is min or max by putting a=.999; b=1.001 ⇒ c=1.0000005 ⇒ lhs >3 ⇒ proven I know you want a different kind of proof but this is the easiest path
$$\mathrm{due}\:\mathrm{to}\:\mathrm{symmetry}\:\mathrm{extremes}\:\mathrm{at}\:{a}={b}={c}\:\Rightarrow \\ $$$${ab}+{bc}+{ac}=\mathrm{3}\:\Leftrightarrow\:\mathrm{3}{a}^{\mathrm{2}} =\mathrm{3}\:\Rightarrow\:{a}=\pm\mathrm{1} \\ $$$$\mathrm{but}\:{a}>\mathrm{0}\:\Rightarrow\:{a}={b}={c}=\mathrm{1} \\ $$$$\mathrm{the}\:\mathrm{inequation}\:\mathrm{with}\:{a}={b}={c}\:\mathrm{turns}\:\mathrm{into} \\ $$$$\mathrm{3}{a}\geqslant\mathrm{3}\:\Rightarrow\:\mathrm{true}\:\mathrm{for}\:{a}=\mathrm{1} \\ $$$$\mathrm{now}\:\mathrm{test}\:\mathrm{if}\:\mathrm{this}\:\mathrm{is}\:\mathrm{min}\:\mathrm{or}\:\mathrm{max}\:\mathrm{by}\:\mathrm{putting} \\ $$$${a}=.\mathrm{999};\:{b}=\mathrm{1}.\mathrm{001}\:\Rightarrow\:{c}=\mathrm{1}.\mathrm{0000005} \\ $$$$\Rightarrow\:\mathrm{lhs}\:>\mathrm{3} \\ $$$$\Rightarrow\:\mathrm{proven} \\ $$$$\mathrm{I}\:\mathrm{know}\:\mathrm{you}\:\mathrm{want}\:\mathrm{a}\:\mathrm{different}\:\mathrm{kind}\:\mathrm{of}\:\mathrm{proof} \\ $$$$\mathrm{but}\:\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{easiest}\:\mathrm{path} \\ $$
Commented by  M±th+et+s last updated on 17/Jun/20
this is a good proof thank you
$${this}\:{is}\:{a}\:{good}\:{proof}\:{thank}\:{you}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *