Question Number 33571 by Joel578 last updated on 19/Apr/18
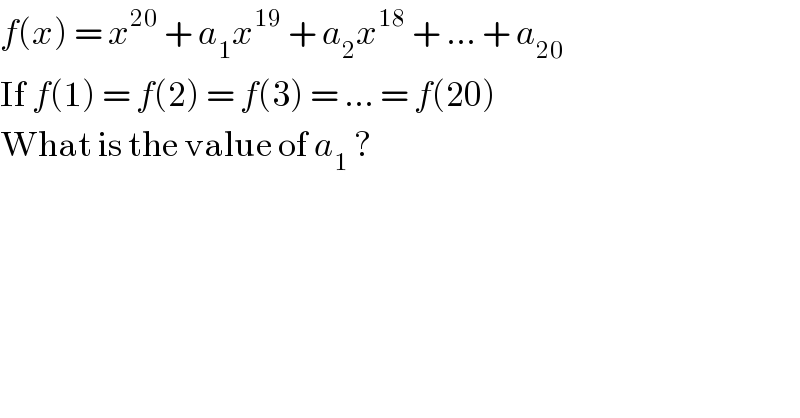
$${f}\left({x}\right)\:=\:{x}^{\mathrm{20}} \:+\:{a}_{\mathrm{1}} {x}^{\mathrm{19}} \:+\:{a}_{\mathrm{2}} {x}^{\mathrm{18}} \:+\:…\:+\:{a}_{\mathrm{20}} \\ $$$$\mathrm{If}\:{f}\left(\mathrm{1}\right)\:=\:{f}\left(\mathrm{2}\right)\:=\:{f}\left(\mathrm{3}\right)\:=\:…\:=\:{f}\left(\mathrm{20}\right) \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{a}_{\mathrm{1}} \:? \\ $$
Answered by MJS last updated on 19/Apr/18
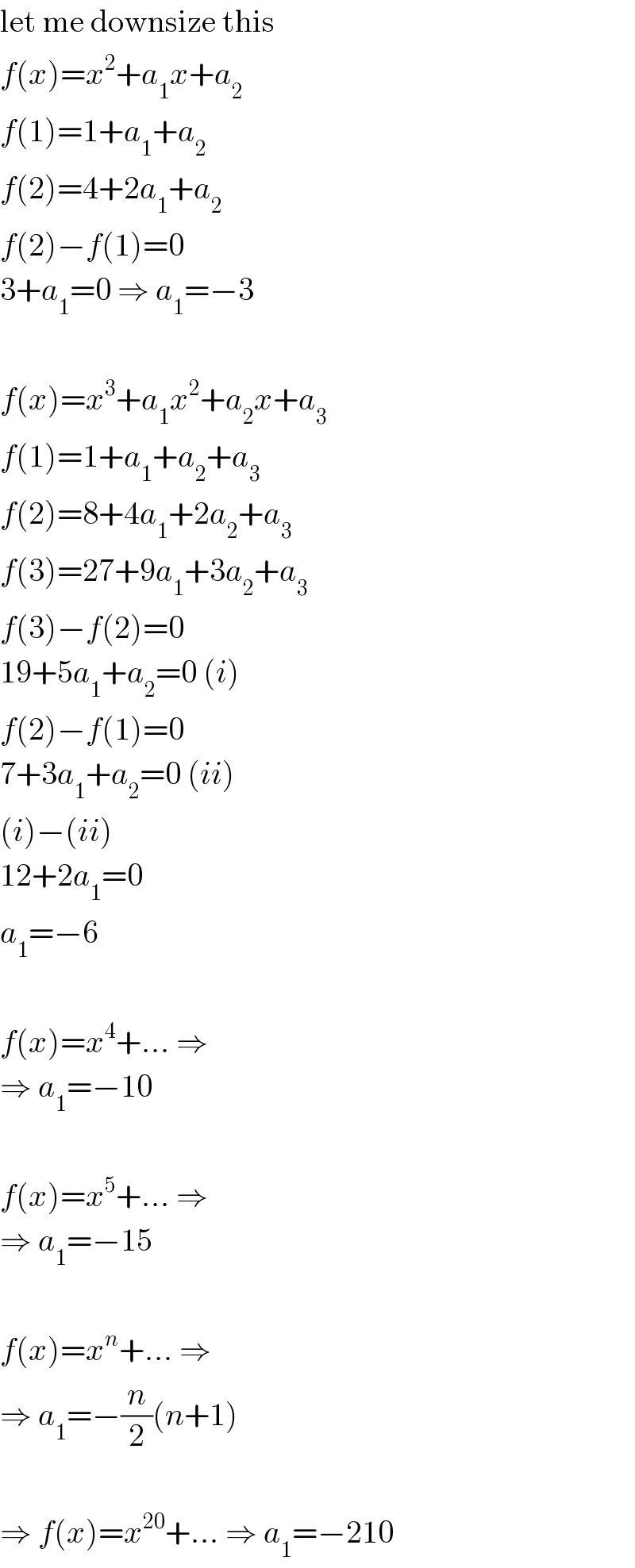
$$\mathrm{let}\:\mathrm{me}\:\mathrm{downsize}\:\mathrm{this} \\ $$$${f}\left({x}\right)={x}^{\mathrm{2}} +{a}_{\mathrm{1}} {x}+{a}_{\mathrm{2}} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1}+{a}_{\mathrm{1}} +{a}_{\mathrm{2}} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{4}+\mathrm{2}{a}_{\mathrm{1}} +{a}_{\mathrm{2}} \\ $$$${f}\left(\mathrm{2}\right)−{f}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{3}+{a}_{\mathrm{1}} =\mathrm{0}\:\Rightarrow\:{a}_{\mathrm{1}} =−\mathrm{3} \\ $$$$ \\ $$$${f}\left({x}\right)={x}^{\mathrm{3}} +{a}_{\mathrm{1}} {x}^{\mathrm{2}} +{a}_{\mathrm{2}} {x}+{a}_{\mathrm{3}} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1}+{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +{a}_{\mathrm{3}} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{8}+\mathrm{4}{a}_{\mathrm{1}} +\mathrm{2}{a}_{\mathrm{2}} +{a}_{\mathrm{3}} \\ $$$${f}\left(\mathrm{3}\right)=\mathrm{27}+\mathrm{9}{a}_{\mathrm{1}} +\mathrm{3}{a}_{\mathrm{2}} +{a}_{\mathrm{3}} \\ $$$${f}\left(\mathrm{3}\right)−{f}\left(\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{19}+\mathrm{5}{a}_{\mathrm{1}} +{a}_{\mathrm{2}} =\mathrm{0}\:\left({i}\right) \\ $$$${f}\left(\mathrm{2}\right)−{f}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{7}+\mathrm{3}{a}_{\mathrm{1}} +{a}_{\mathrm{2}} =\mathrm{0}\:\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right) \\ $$$$\mathrm{12}+\mathrm{2}{a}_{\mathrm{1}} =\mathrm{0} \\ $$$${a}_{\mathrm{1}} =−\mathrm{6} \\ $$$$ \\ $$$${f}\left({x}\right)={x}^{\mathrm{4}} +…\:\Rightarrow \\ $$$$\Rightarrow\:{a}_{\mathrm{1}} =−\mathrm{10} \\ $$$$ \\ $$$${f}\left({x}\right)={x}^{\mathrm{5}} +…\:\Rightarrow \\ $$$$\Rightarrow\:{a}_{\mathrm{1}} =−\mathrm{15} \\ $$$$ \\ $$$${f}\left({x}\right)={x}^{{n}} +…\:\Rightarrow \\ $$$$\Rightarrow\:{a}_{\mathrm{1}} =−\frac{{n}}{\mathrm{2}}\left({n}+\mathrm{1}\right) \\ $$$$ \\ $$$$\Rightarrow\:{f}\left({x}\right)={x}^{\mathrm{20}} +…\:\Rightarrow\:{a}_{\mathrm{1}} =−\mathrm{210} \\ $$
Commented by Joel578 last updated on 20/Apr/18
$${thank}\:{you}\:{very}\:{much} \\ $$
