Question Number 33704 by math khazana by abdo last updated on 22/Apr/18
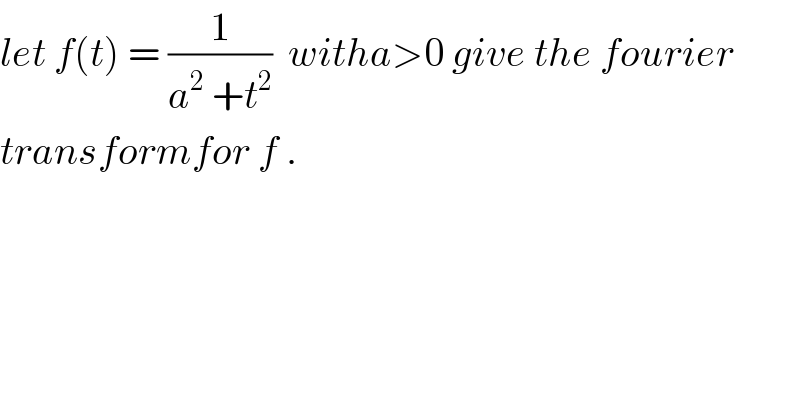
$${let}\:{f}\left({t}\right)\:=\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} \:+{t}^{\mathrm{2}} }\:\:{witha}>\mathrm{0}\:{give}\:{the}\:{fourier} \\ $$$${transformfor}\:{f}\:. \\ $$$$ \\ $$
Commented by prof Abdo imad last updated on 27/Apr/18

$${we}\:{know}\:{that}\:{F}\left({f}\left({x}\right)\right)\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}\pi}}\:\int_{−\infty} ^{+\infty} {f}\left({t}\right)\:{e}^{−{ixt}} {dt}\:{so} \\ $$$${for}\:{f}\left({x}\right)=\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:{we}\:{get} \\ $$$${F}\left({f}\left({x}\right)\right)=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}\pi}}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{e}^{−{ixt}} }{{a}^{\mathrm{2}} \:+{t}^{\mathrm{2}} }\:{dt}\:\:{let}\:{consider}\:{the} \\ $$$${complex}\:{function}\:\varphi\left({z}\right)\:=\:\:\frac{{e}^{−{ixz}} }{{z}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }\:{the}\:{poles}\:{of} \\ $$$$\varphi\:{are}\:{ia}\:{and}\:−{ia}\:\left({simples}\right)\:{so} \\ $$$$\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{ia}\right) \\ $$$$\varphi\left({z}\right)=\:\:\frac{{e}^{−{ixz}} }{\left({z}−{ia}\right)\left({z}+{ia}\right)}\:\Rightarrow{Res}\left(\varphi,{ia}\right)=\:\frac{{e}^{−{ix}\left({ia}\right)} }{\mathrm{2}{ia}} \\ $$$$=\:\:\frac{{e}^{{ax}} }{\mathrm{2}{ia}}\:\Rightarrow\:\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\frac{{e}^{{ax}} }{\mathrm{2}{ia}}\:=\:\frac{\pi}{{a}}\:{e}^{{ax}} \:\Rightarrow \\ $$$${F}\left({f}\left({x}\right)\right)=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}\pi}}\:\frac{\pi}{{a}}\:{e}^{{ax}} \:=\sqrt{\frac{\pi^{\mathrm{2}} }{\mathrm{2}\pi}}\:\:\frac{{e}^{{ax}} }{{a}} \\ $$$$\bigstar{F}\left({f}\left({x}\right)\left({t}\right)=\:\sqrt{\frac{\pi}{\mathrm{2}}}\:\:\frac{{e}^{{ax}} }{{a}}\:\bigstar\right. \\ $$
