Question Number 33744 by prof Abdo imad last updated on 23/Apr/18
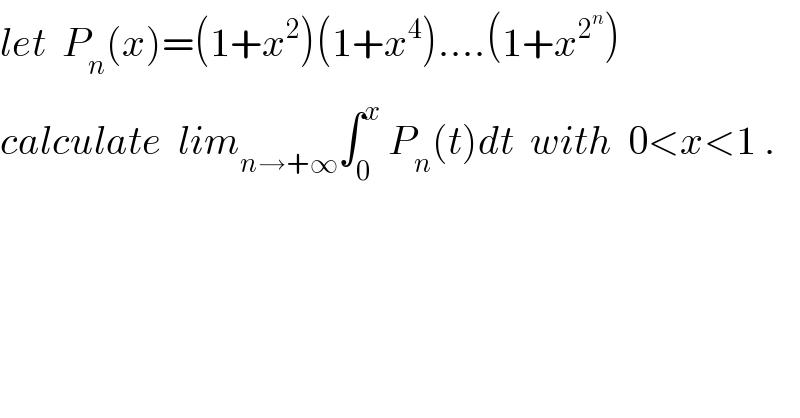
$${let}\:\:{P}_{{n}} \left({x}\right)=\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{4}} \right)….\left(\mathrm{1}+{x}^{\mathrm{2}^{{n}} } \right) \\ $$$${calculate}\:\:{lim}_{{n}\rightarrow+\infty} \int_{\mathrm{0}} ^{{x}} \:{P}_{{n}} \left({t}\right){dt}\:\:{with}\:\:\mathrm{0}<{x}<\mathrm{1}\:. \\ $$
Commented by prof Abdo imad last updated on 25/Apr/18
![we have proved that P_n (t) = ((1−t^2^(n+1) )/(1−t^2 )) ⇒ ∫_0 ^x P_n (t)dt = ∫_0 ^x ((1−t^2^(n+1) )/(1−t^2 ))dt = ∫_0 ^x (dt/(1−t^2 )) −∫_0 ^x (t^2^(n+1) /(1−t^2 )) dt but lim_(n→+∞) ∫_0 ^x (t^2^(n+1) /(1−t^2 )) dt =0 because 0≤ ⇒t≤x<1 ⇒ lim_(n→+∞) ∫_0 ^x P_n (t)dt = ∫_0 ^x (dt/(1−t^2 )) =(1/2) ∫_0 ^x ( (1/(1−t)) +(1/(1+t)))dt =[(1/2)ln∣((1+t)/(1−t))∣]_0 ^c =(1/2) ln∣ ((1+x)/(1−x))∣ .](https://www.tinkutara.com/question/Q33806.png)
$${we}\:{have}\:{proved}\:{that}\:\:{P}_{{n}} \left({t}\right)\:=\:\frac{\mathrm{1}−{t}^{\mathrm{2}^{{n}+\mathrm{1}} } }{\mathrm{1}−{t}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{{x}} \:\:{P}_{{n}} \left({t}\right){dt}\:=\:\int_{\mathrm{0}} ^{{x}} \:\:\frac{\mathrm{1}−{t}^{\mathrm{2}^{{n}+\mathrm{1}} } }{\mathrm{1}−{t}^{\mathrm{2}} }{dt} \\ $$$$=\:\int_{\mathrm{0}} ^{{x}} \:\:\:\frac{{dt}}{\mathrm{1}−{t}^{\mathrm{2}} }\:\:−\int_{\mathrm{0}} ^{{x}} \:\:\:\frac{{t}^{\mathrm{2}^{{n}+\mathrm{1}} } }{\mathrm{1}−{t}^{\mathrm{2}} }\:{dt}\:\:{but} \\ $$$${lim}_{{n}\rightarrow+\infty} \:\int_{\mathrm{0}} ^{{x}} \:\:\:\frac{{t}^{\mathrm{2}^{{n}+\mathrm{1}} } }{\mathrm{1}−{t}^{\mathrm{2}} }\:{dt}\:=\mathrm{0}\:{because}\:\mathrm{0}\leqslant\:\Rightarrow{t}\leqslant{x}<\mathrm{1} \\ $$$$\Rightarrow\:{lim}_{{n}\rightarrow+\infty} \:\:\int_{\mathrm{0}} ^{{x}} \:\:{P}_{{n}} \left({t}\right){dt}\:=\:\int_{\mathrm{0}} ^{{x}} \:\frac{{dt}}{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{x}} \:\left(\:\frac{\mathrm{1}}{\mathrm{1}−{t}}\:+\frac{\mathrm{1}}{\mathrm{1}+{t}}\right){dt}\:=\left[\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\mid\right]_{\mathrm{0}} ^{{c}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:{ln}\mid\:\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\mid\:. \\ $$
