Menu Close

Prove-that-if-circum-circle-and-in-circle-of-a-triangle-are-concentric-the-triangle-is-an-equalateral-triangle-

Tinku Tara 0 Comments
Pin




Question Number 33756 by Rasheed.Sindhi last updated on 23/Apr/18
Prove that if circum-circle and in-circle of a triangle are concentric, the triangle is an equalateral triangle.
$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{if}\:\boldsymbol{\mathrm{circum}}-\boldsymbol{\mathrm{circle}}\:\mathrm{and} \\ $$$$\boldsymbol{\mathrm{in}}-\boldsymbol{\mathrm{circle}}\:\mathrm{of}\:\mathrm{a}\:\mathrm{triangle}\:\mathrm{are}\:\boldsymbol{\mathrm{concentric}}, \\ $$$$\mathrm{the}\:\mathrm{triangle}\:\mathrm{is}\:\mathrm{an}\:\boldsymbol{\mathrm{equalateral}}\:\boldsymbol{\mathrm{triangle}}. \\ $$
Answered by MJS last updated on 23/Apr/18
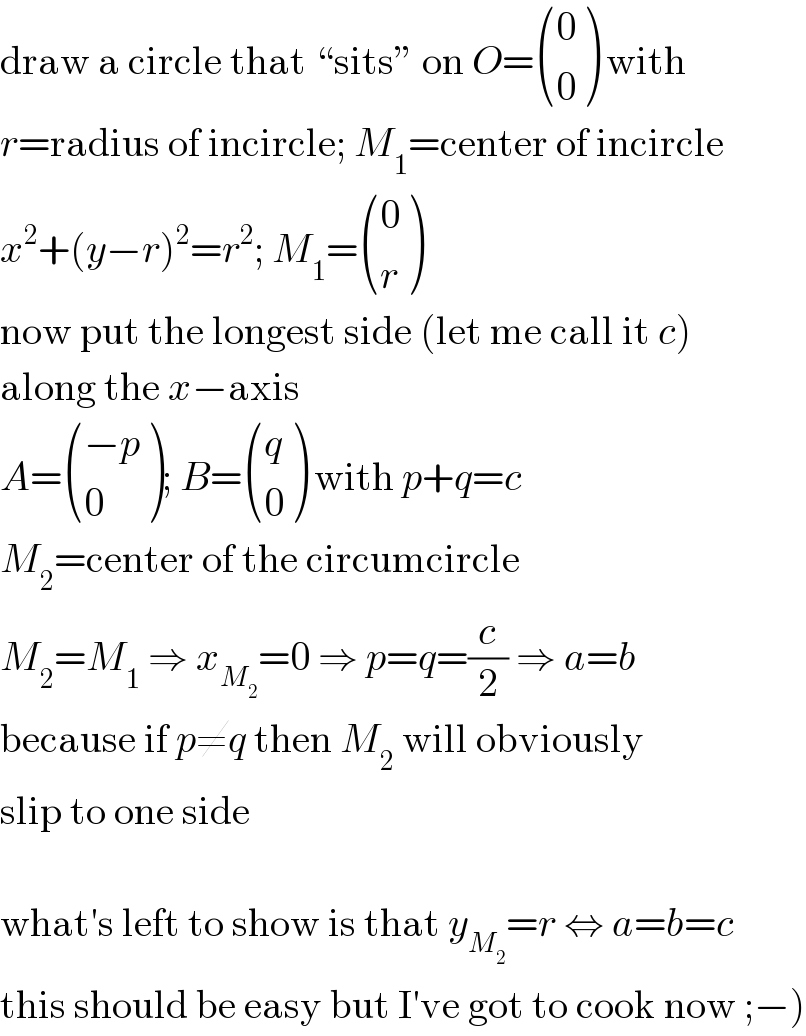
draw a circle that “sits” on O= ((0),(0) ) with r=radius of incircle; M_1 =center of incircle x^2 +(y−r)^2 =r^2 ; M_1 = ((0),(r) ) now put the longest side (let me call it c) along the x−axis A= (((−p)),(0) ); B= ((q),(0) ) with p+q=c M_2 =center of the circumcircle M_2 =M_1 ⇒ x_M_2 =0 ⇒ p=q=(c/2) ⇒ a=b because if p≠q then M_2 will obviously slip to one side what′s left to show is that y_M_2 =r ⇔ a=b=c this should be easy but I′ve got to cook now ;−)
$$\mathrm{draw}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{that}\:“\mathrm{sits}''\:\mathrm{on}\:{O}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\mathrm{with} \\ $$$${r}=\mathrm{radius}\:\mathrm{of}\:\mathrm{incircle};\:{M}_{\mathrm{1}} =\mathrm{center}\:\mathrm{of}\:\mathrm{incircle} \\ $$$${x}^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} ;\:{M}_{\mathrm{1}} =\begin{pmatrix}{\mathrm{0}}\\{{r}}\end{pmatrix} \\ $$$$\mathrm{now}\:\mathrm{put}\:\mathrm{the}\:\mathrm{longest}\:\mathrm{side}\:\left(\mathrm{let}\:\mathrm{me}\:\mathrm{call}\:\mathrm{it}\:{c}\right) \\ $$$$\mathrm{along}\:\mathrm{the}\:{x}−\mathrm{axis} \\ $$$${A}=\begin{pmatrix}{−{p}}\\{\mathrm{0}}\end{pmatrix};\:{B}=\begin{pmatrix}{{q}}\\{\mathrm{0}}\end{pmatrix}\:\mathrm{with}\:{p}+{q}={c} \\ $$$${M}_{\mathrm{2}} =\mathrm{center}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circumcircle} \\ $$$${M}_{\mathrm{2}} ={M}_{\mathrm{1}} \:\Rightarrow\:{x}_{{M}_{\mathrm{2}} } =\mathrm{0}\:\Rightarrow\:{p}={q}=\frac{{c}}{\mathrm{2}}\:\Rightarrow\:{a}={b} \\ $$$$\mathrm{because}\:\mathrm{if}\:{p}\neq{q}\:\mathrm{then}\:{M}_{\mathrm{2}} \:\mathrm{will}\:\mathrm{obviously} \\ $$$$\mathrm{slip}\:\mathrm{to}\:\mathrm{one}\:\mathrm{side} \\ $$$$ \\ $$$$\mathrm{what}'\mathrm{s}\:\mathrm{left}\:\mathrm{to}\:\mathrm{show}\:\mathrm{is}\:\mathrm{that}\:{y}_{{M}_{\mathrm{2}} } ={r}\:\Leftrightarrow\:{a}={b}={c} \\ $$$$\left.\mathrm{this}\:\mathrm{should}\:\mathrm{be}\:\mathrm{easy}\:\mathrm{but}\:\mathrm{I}'\mathrm{ve}\:\mathrm{got}\:\mathrm{to}\:\mathrm{cook}\:\mathrm{now}\:;−\right) \\ $$
Commented by Rasheed.Sindhi last updated on 23/Apr/18
ŦΉΛПKS Λ LӨŦ SIЯ!

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *