Question Number 33764 by .none. last updated on 23/Apr/18
![2x−y=(1/( (√5)−2)) x+2y=(1/( (√5)+2)) [3x^2 −8xy−3y^2 ]?](https://www.tinkutara.com/question/Q33764.png)
$$\mathrm{2}{x}−{y}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}−\mathrm{2}} \\ $$$${x}+\mathrm{2}{y}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}+\mathrm{2}} \\ $$$$\left[\mathrm{3}{x}^{\mathrm{2}} −\mathrm{8}{xy}−\mathrm{3}{y}^{\mathrm{2}} \right]? \\ $$
Answered by Rasheed.Sindhi last updated on 23/Apr/18
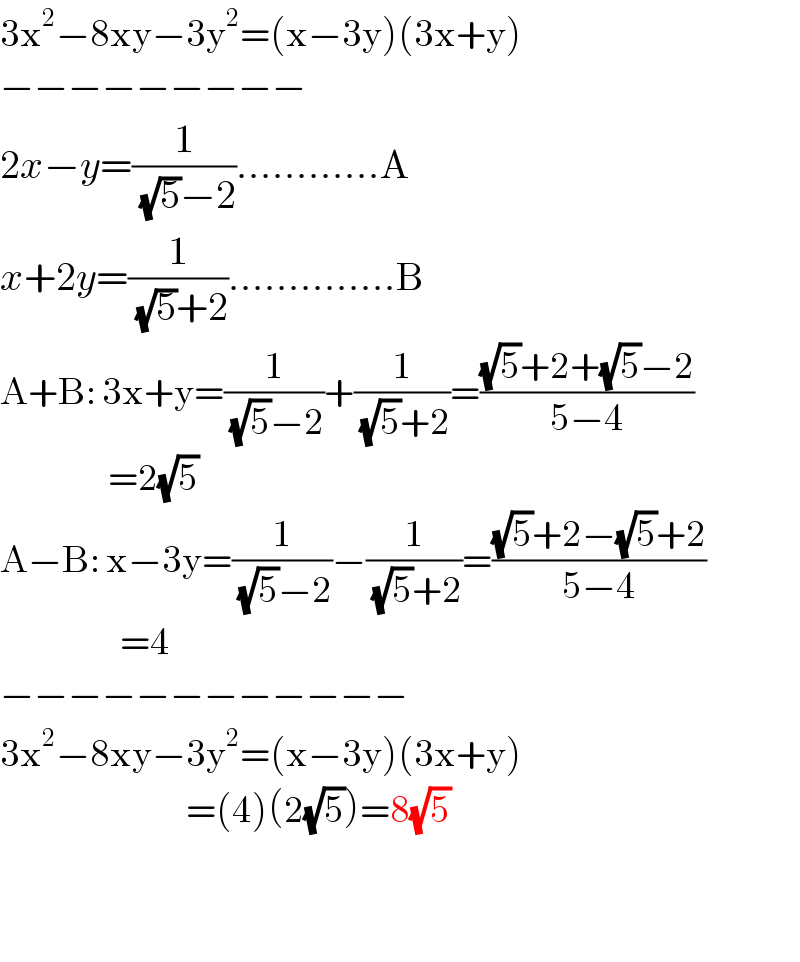
$$\mathrm{3x}^{\mathrm{2}} −\mathrm{8xy}−\mathrm{3y}^{\mathrm{2}} =\left(\mathrm{x}−\mathrm{3y}\right)\left(\mathrm{3x}+\mathrm{y}\right) \\ $$$$−−−−−−−−− \\ $$$$\mathrm{2}{x}−{y}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}−\mathrm{2}}…………\mathrm{A} \\ $$$${x}+\mathrm{2}{y}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}+\mathrm{2}}…………..\mathrm{B} \\ $$$$\mathrm{A}+\mathrm{B}:\:\mathrm{3x}+\mathrm{y}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}−\mathrm{2}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}+\mathrm{2}}=\frac{\sqrt{\mathrm{5}}+\mathrm{2}+\sqrt{\mathrm{5}}−\mathrm{2}}{\mathrm{5}−\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$\mathrm{A}−\mathrm{B}:\:\mathrm{x}−\mathrm{3y}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}−\mathrm{2}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}+\mathrm{2}}=\frac{\sqrt{\mathrm{5}}+\mathrm{2}−\sqrt{\mathrm{5}}+\mathrm{2}}{\mathrm{5}−\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{4} \\ $$$$−−−−−−−−−−−− \\ $$$$\mathrm{3x}^{\mathrm{2}} −\mathrm{8xy}−\mathrm{3y}^{\mathrm{2}} =\left(\mathrm{x}−\mathrm{3y}\right)\left(\mathrm{3x}+\mathrm{y}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{4}\right)\left(\mathrm{2}\sqrt{\mathrm{5}}\right)=\mathrm{8}\sqrt{\mathrm{5}} \\ $$$$ \\ $$$$ \\ $$
Commented by .none. last updated on 23/Apr/18
$${Thanks}\:{to}\:{you},{i}\:{can}\:{solve}\:{this}\:{now} \\ $$
