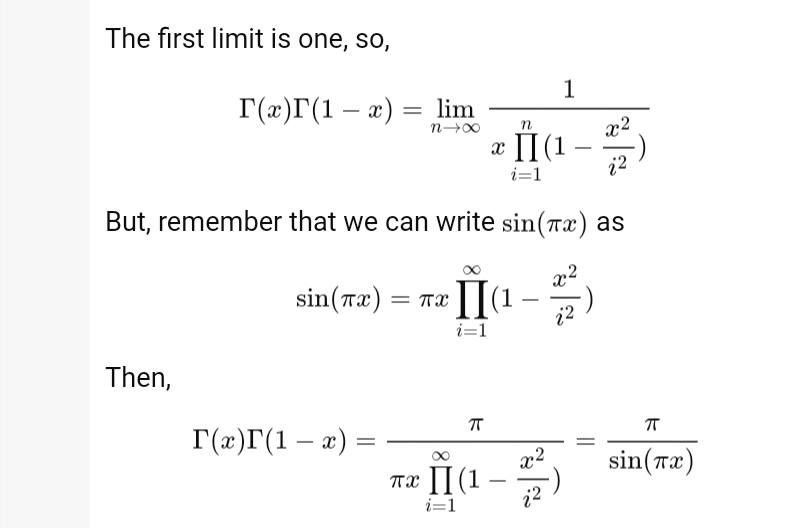Question Number 33895 by math khazana by abdo last updated on 26/Apr/18
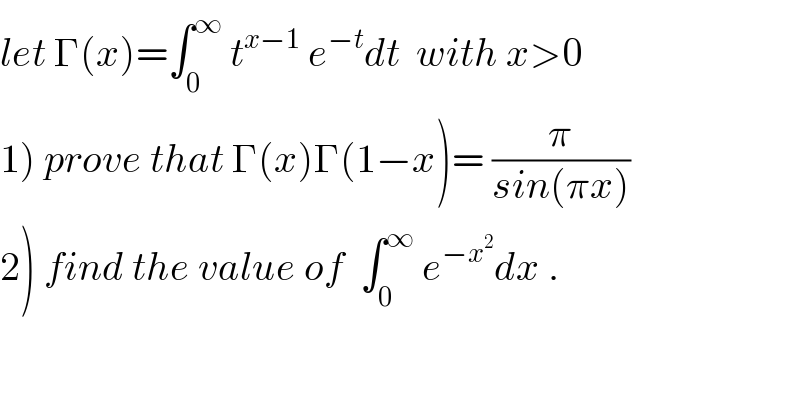
$${let}\:\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:{t}^{{x}−\mathrm{1}} \:{e}^{−{t}} {dt}\:\:{with}\:{x}>\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{prove}\:{that}\:\Gamma\left({x}\right)\Gamma\left(\mathrm{1}−{x}\right)=\:\frac{\pi}{{sin}\left(\pi{x}\right)} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{x}^{\mathrm{2}} } {dx}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Apr/18
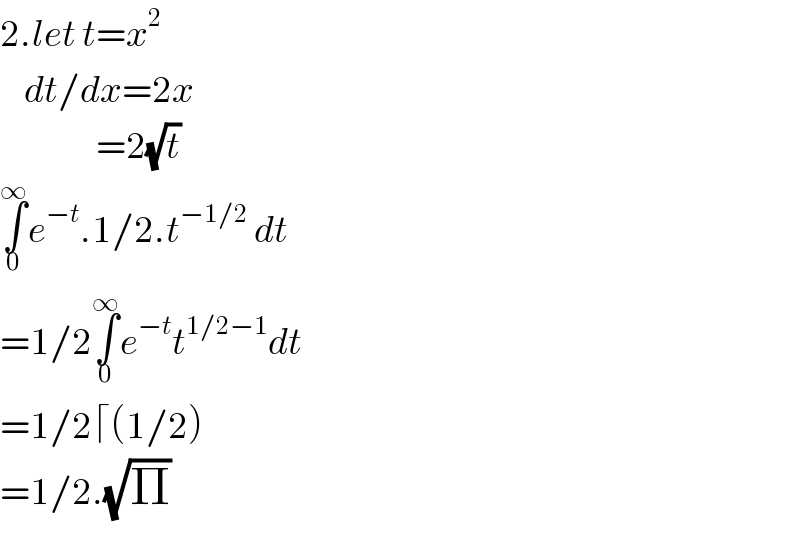
$$\mathrm{2}.{let}\:{t}={x}^{\mathrm{2}} \\ $$$$\:\:\:\:{dt}/{dx}=\mathrm{2}{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\sqrt{{t}} \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}{e}^{−{t}} .\mathrm{1}/\mathrm{2}.{t}^{−\mathrm{1}/\mathrm{2}} \:{dt} \\ $$$$=\mathrm{1}/\mathrm{2}\underset{\mathrm{0}} {\overset{\infty} {\int}}{e}^{−{t}} {t}^{\mathrm{1}/\mathrm{2}−\mathrm{1}} {dt} \\ $$$$=\mathrm{1}/\mathrm{2}\lceil\left(\mathrm{1}/\mathrm{2}\right) \\ $$$$=\mathrm{1}/\mathrm{2}.\sqrt{\Pi} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Apr/18

Commented by tanmay.chaudhury50@gmail.com last updated on 28/Apr/18

$${do}\:{you}\:{like}\:{the}\:{different}\:{method}\:{to}\:{find}\:{the}\:{solution} \\ $$$$…{it}\:{is}\:{not}\:{available}\:{in}\:{apps}.. \\ $$
Commented by NECx last updated on 28/Apr/18
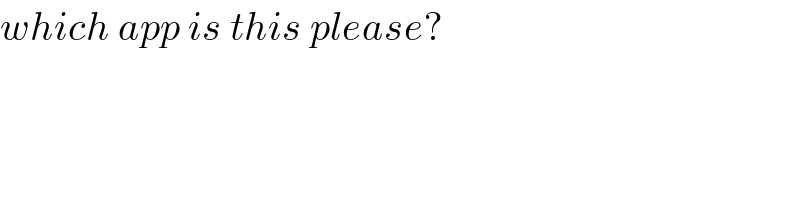
$${which}\:{app}\:{is}\:{this}\:{please}? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 28/Apr/18