Question Number 134331 by Mikael_786 last updated on 02/Mar/21
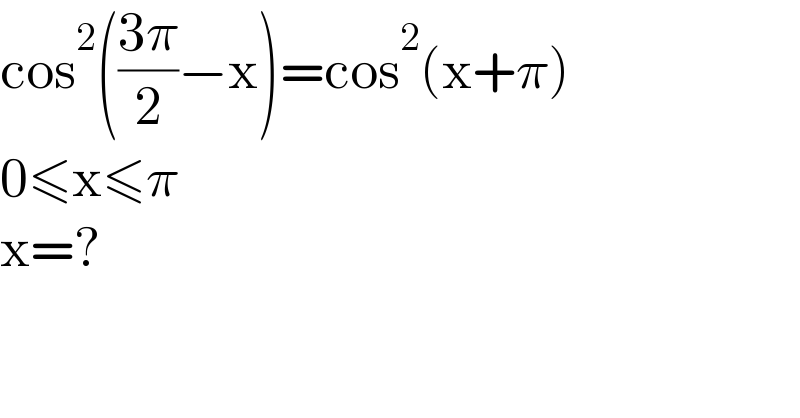
$$\mathrm{cos}^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{2}}−\mathrm{x}\right)=\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}+\pi\right) \\ $$$$\mathrm{0}\leqslant\mathrm{x}\leqslant\pi \\ $$$$\mathrm{x}=? \\ $$
Answered by EDWIN88 last updated on 02/Mar/21
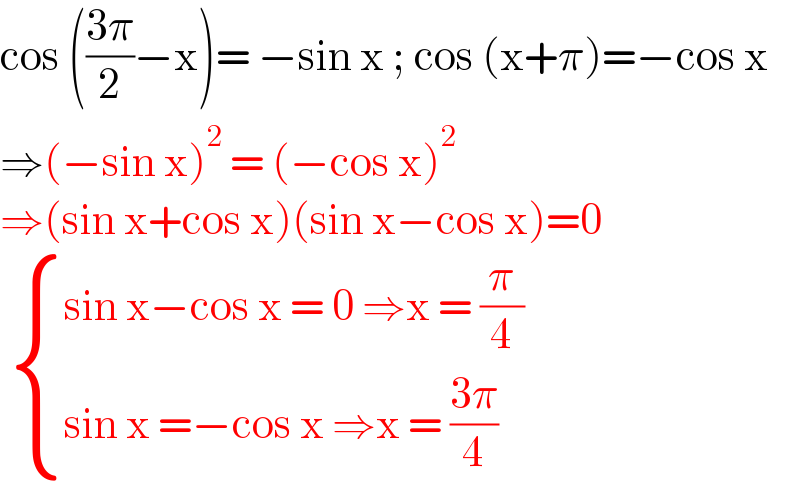
$$\mathrm{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{2}}−\mathrm{x}\right)=\:−\mathrm{sin}\:\mathrm{x}\:;\:\mathrm{cos}\:\left(\mathrm{x}+\pi\right)=−\mathrm{cos}\:\mathrm{x} \\ $$$$\Rightarrow\left(−\mathrm{sin}\:\mathrm{x}\right)^{\mathrm{2}} \:=\:\left(−\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\right)\left(\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}\right)=\mathrm{0} \\ $$$$\:\begin{cases}{\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{0}\:\Rightarrow\mathrm{x}\:=\:\frac{\pi}{\mathrm{4}}}\\{\mathrm{sin}\:\mathrm{x}\:=−\mathrm{cos}\:\mathrm{x}\:\Rightarrow\mathrm{x}\:=\:\frac{\mathrm{3}\pi}{\mathrm{4}}}\end{cases} \\ $$
