Menu Close

let-u-n-n-1-n-1-n-n-n-n-1-find-lim-n-u-n-

Tinku Tara 0 Comments
Pin




Question Number 34226 by abdo imad last updated on 03/May/18
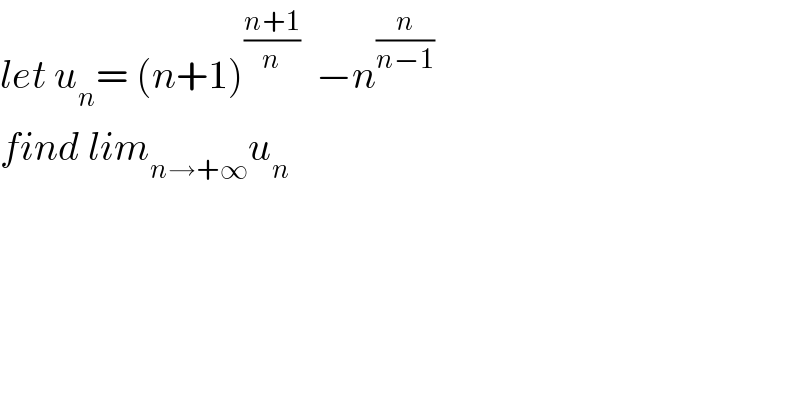
let u_n = (n+1)^((n+1)/n) −n^(n/(n−1)) find lim_(n→+∞) u_n
$${let}\:{u}_{{n}} =\:\left({n}+\mathrm{1}\right)^{\frac{{n}+\mathrm{1}}{{n}}} \:\:−{n}^{\frac{{n}}{{n}−\mathrm{1}}} \\ $$$${find}\:{lim}_{{n}\rightarrow+\infty} {u}_{{n}} \\ $$
Commented by abdo mathsup 649 cc last updated on 05/May/18
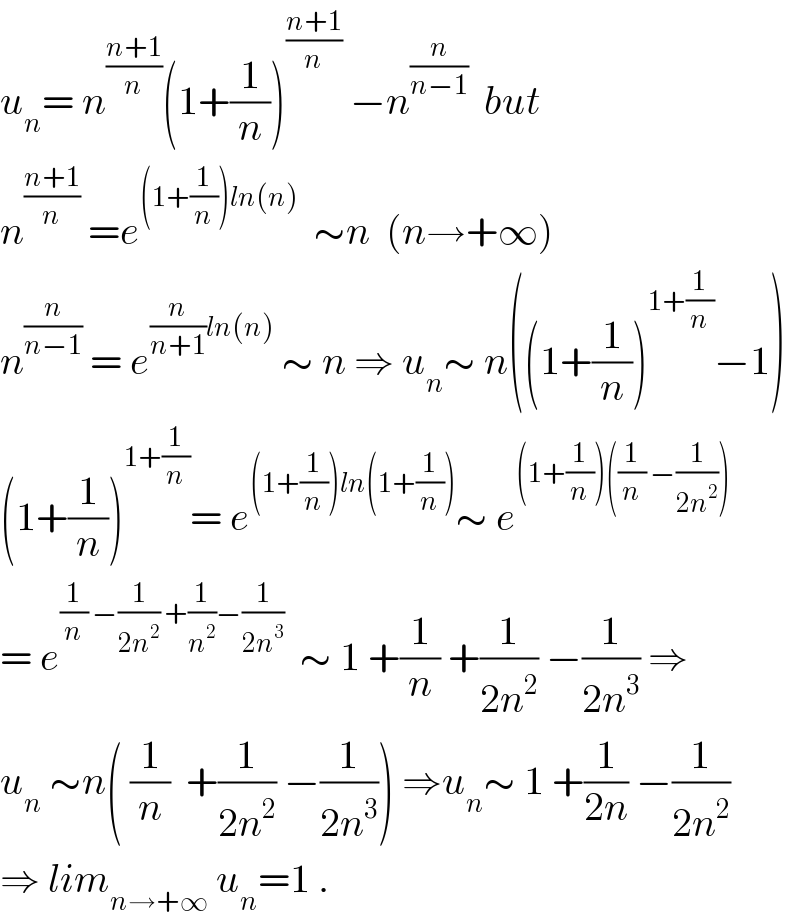
u_n = n^((n+1)/n) (1+(1/n))^((n+1)/n) −n^(n/(n−1)) but n^((n+1)/n) =e^((1+(1/n))ln(n)) ∼n (n→+∞) n^(n/(n−1)) = e^((n/(n+1))ln(n)) ∼ n ⇒ u_n ∼ n((1+(1/n))^(1+(1/n)) −1) (1+(1/n))^(1+(1/n)) = e^((1+(1/n))ln(1+(1/n))) ∼ e^((1+(1/n))((1/n) −(1/(2n^2 )))) = e^((1/n) −(1/(2n^2 )) +(1/n^2 )−(1/(2n^3 ))) ∼ 1 +(1/n) +(1/(2n^2 )) −(1/(2n^3 )) ⇒ u_n ∼n( (1/n) +(1/(2n^2 )) −(1/(2n^3 ))) ⇒u_n ∼ 1 +(1/(2n)) −(1/(2n^2 )) ⇒ lim_(n→+∞) u_n =1 .
$${u}_{{n}} =\:{n}^{\frac{{n}+\mathrm{1}}{{n}}} \left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{\frac{{n}+\mathrm{1}}{{n}}} \:−{n}^{\frac{{n}}{{n}−\mathrm{1}}} \:\:{but} \\ $$$${n}^{\frac{{n}+\mathrm{1}}{{n}}} \:={e}^{\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right){ln}\left({n}\right)} \:\:\sim{n}\:\:\left({n}\rightarrow+\infty\right) \\ $$$${n}^{\frac{{n}}{{n}−\mathrm{1}}} \:=\:{e}^{\frac{{n}}{{n}+\mathrm{1}}{ln}\left({n}\right)} \:\sim\:{n}\:\Rightarrow\:{u}_{{n}} \sim\:{n}\left(\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{\mathrm{1}+\frac{\mathrm{1}}{{n}}} −\mathrm{1}\right) \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{\mathrm{1}+\frac{\mathrm{1}}{{n}}} =\:{e}^{\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right){ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)} \sim\:{e}^{\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)\left(\frac{\mathrm{1}}{{n}}\:−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }\right)} \\ $$$$=\:{e}^{\frac{\mathrm{1}}{{n}}\:−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{3}} }} \:\:\sim\:\mathrm{1}\:+\frac{\mathrm{1}}{{n}}\:+\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{3}} }\:\Rightarrow \\ $$$${u}_{{n}} \:\sim{n}\left(\:\frac{\mathrm{1}}{{n}}\:\:+\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{3}} }\right)\:\Rightarrow{u}_{{n}} \sim\:\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{2}{n}}\:−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{lim}_{{n}\rightarrow+\infty} \:{u}_{{n}} =\mathrm{1}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *