Question Number 165322 by Ari last updated on 29/Jan/22
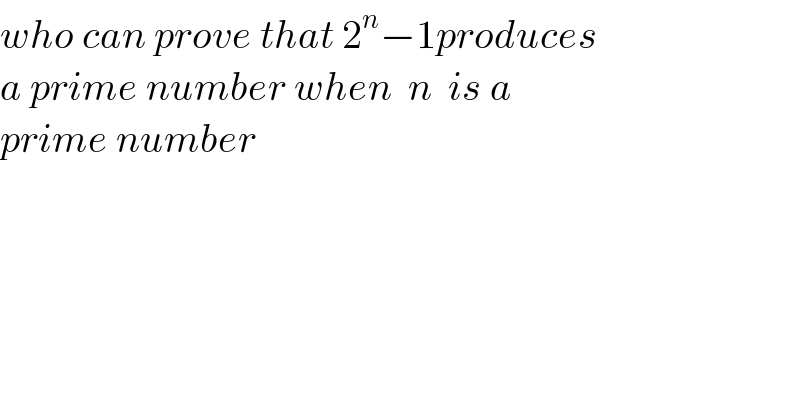
$${who}\:{can}\:{prove}\:{that}\:\mathrm{2}^{{n}} −\mathrm{1}{produces} \\ $$$${a}\:{prime}\:{number}\:{when}\:\:{n}\:\:{is}\:{a}\: \\ $$$${prime}\:{number} \\ $$
Commented by mr W last updated on 30/Jan/22
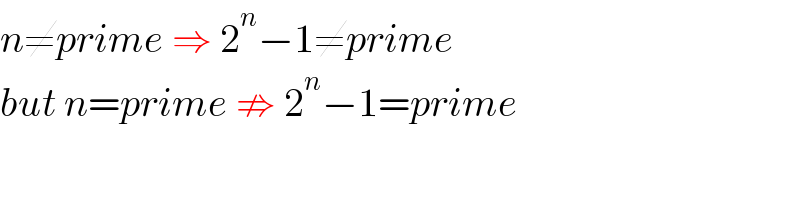
$${n}\neq{prime}\:\Rightarrow\:\mathrm{2}^{{n}} −\mathrm{1}\neq{prime} \\ $$$${but}\:{n}={prime}\:\nRightarrow\:\mathrm{2}^{{n}} −\mathrm{1}={prime} \\ $$
Commented by mr W last updated on 30/Jan/22

$${primes}\:{of}\:{type}\:\mathrm{2}^{{n}} −\mathrm{1}\:{with}\:{n}={prime} \\ $$$${are}\:{called}\:{Mersene}\:{primes}.\:{it}\:{doesn}'{t} \\ $$$${mean}\:{that}\:\mathrm{2}^{{n}} −\mathrm{1}\:{is}\:{always}\:\:{prime}\:{for}\: \\ $$$${any}\:{prime}\:{n}.\:\mathrm{2}^{{n}} −\mathrm{1}\:{is}\:{prime}\:{only}\:{for} \\ $$$${some}\:{primes}\:{n}.\:{the}\:{largest}\:{known}\:{n}\: \\ $$$${is}\:\mathrm{82}\:\mathrm{589}\:\mathrm{933}\:{which}\:{was}\:{found}\:{in}\:\mathrm{2018}. \\ $$
Answered by JDamian last updated on 29/Jan/22
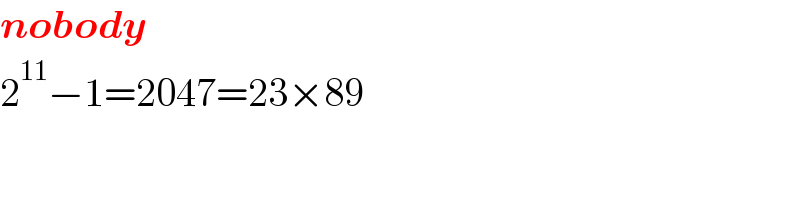
$$\boldsymbol{{nobody}} \\ $$$$\mathrm{2}^{\mathrm{11}} −\mathrm{1}=\mathrm{2047}=\mathrm{23}×\mathrm{89} \\ $$
Commented by mr W last updated on 30/Jan/22
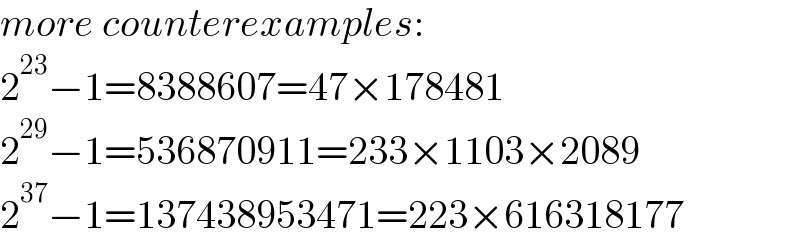
$${more}\:{counterexamples}: \\ $$$$\mathrm{2}^{\mathrm{23}} −\mathrm{1}=\mathrm{8388607}=\mathrm{47}×\mathrm{178481} \\ $$$$\mathrm{2}^{\mathrm{29}} −\mathrm{1}=\mathrm{536870911}=\mathrm{233}×\mathrm{1103}×\mathrm{2089} \\ $$$$\mathrm{2}^{\mathrm{37}} −\mathrm{1}=\mathrm{137438953471}=\mathrm{223}×\mathrm{616318177} \\ $$
