Question Number 165381 by mathlove last updated on 31/Jan/22

Commented by MJS_new last updated on 02/Feb/22

$$\mathrm{we}\:\mathrm{have}\:\mathrm{only}\:\mathrm{one}\:\mathrm{equation}\:\mathrm{for}\:\mathrm{2}\:\mathrm{unknowns} \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{unique}\:\mathrm{solution}. \\ $$
Answered by mahdipoor last updated on 01/Feb/22
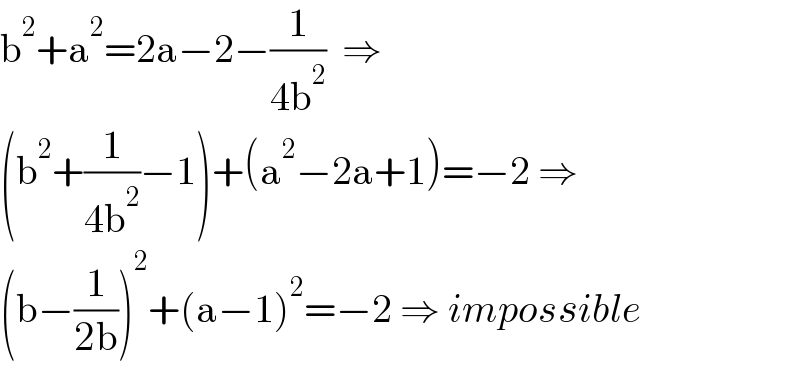
$$\mathrm{b}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} =\mathrm{2a}−\mathrm{2}−\frac{\mathrm{1}}{\mathrm{4b}^{\mathrm{2}} }\:\:\Rightarrow \\ $$$$\left(\mathrm{b}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4b}^{\mathrm{2}} }−\mathrm{1}\right)+\left(\mathrm{a}^{\mathrm{2}} −\mathrm{2a}+\mathrm{1}\right)=−\mathrm{2}\:\Rightarrow \\ $$$$\left(\mathrm{b}−\frac{\mathrm{1}}{\mathrm{2b}}\right)^{\mathrm{2}} +\left(\mathrm{a}−\mathrm{1}\right)^{\mathrm{2}} =−\mathrm{2}\:\Rightarrow\:{impossible} \\ $$
Commented by som(math1967) last updated on 01/Feb/22
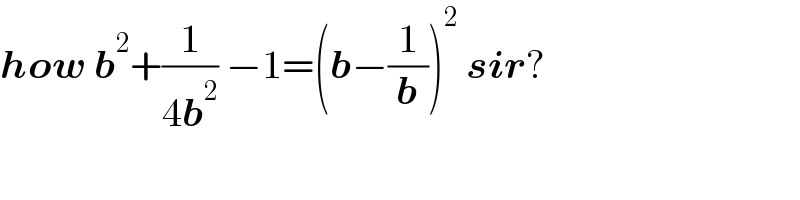
$$\boldsymbol{{how}}\:\boldsymbol{{b}}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}\boldsymbol{{b}}^{\mathrm{2}} }\:−\mathrm{1}=\left(\boldsymbol{{b}}−\frac{\mathrm{1}}{\boldsymbol{{b}}}\right)^{\mathrm{2}} \:\boldsymbol{{sir}}? \\ $$
Commented by mahdipoor last updated on 01/Feb/22
$${thanks}\:{for}\:{your}\:{not} \\ $$
Answered by som(math1967) last updated on 01/Feb/22
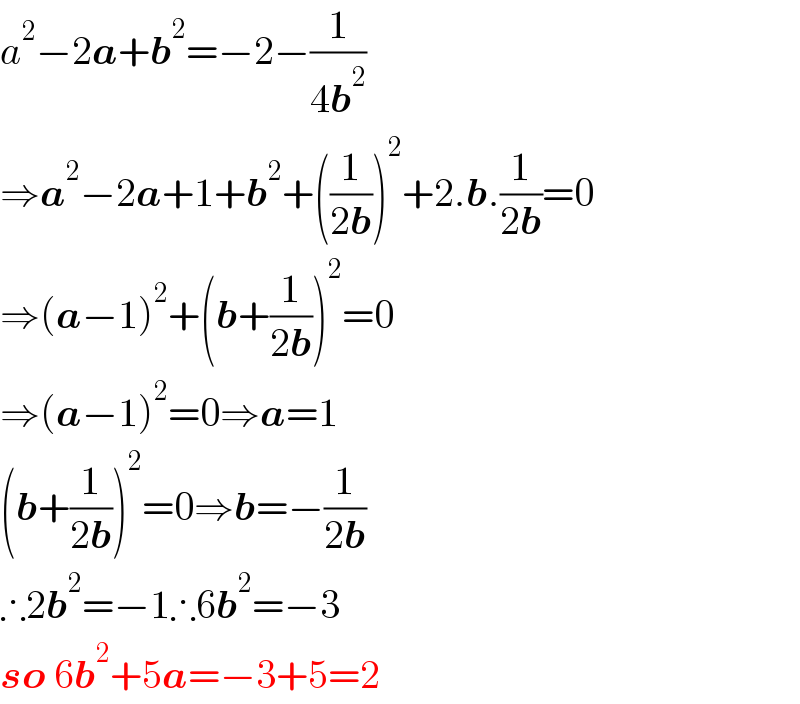
$${a}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{a}}+\boldsymbol{{b}}^{\mathrm{2}} =−\mathrm{2}−\frac{\mathrm{1}}{\mathrm{4}\boldsymbol{{b}}^{\mathrm{2}} } \\ $$$$\Rightarrow\boldsymbol{{a}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{a}}+\mathrm{1}+\boldsymbol{{b}}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{b}}}\right)^{\mathrm{2}} +\mathrm{2}.\boldsymbol{{b}}.\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{b}}}=\mathrm{0} \\ $$$$\Rightarrow\left(\boldsymbol{{a}}−\mathrm{1}\right)^{\mathrm{2}} +\left(\boldsymbol{{b}}+\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{b}}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\left(\boldsymbol{{a}}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0}\Rightarrow\boldsymbol{{a}}=\mathrm{1} \\ $$$$\left(\boldsymbol{{b}}+\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{b}}}\right)^{\mathrm{2}} =\mathrm{0}\Rightarrow\boldsymbol{{b}}=−\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{b}}} \\ $$$$\therefore\mathrm{2}\boldsymbol{{b}}^{\mathrm{2}} =−\mathrm{1}\therefore\mathrm{6}\boldsymbol{{b}}^{\mathrm{2}} =−\mathrm{3} \\ $$$$\boldsymbol{{so}}\:\mathrm{6}\boldsymbol{{b}}^{\mathrm{2}} +\mathrm{5}\boldsymbol{{a}}=−\mathrm{3}+\mathrm{5}=\mathrm{2} \\ $$
Commented by mahdipoor last updated on 01/Feb/22
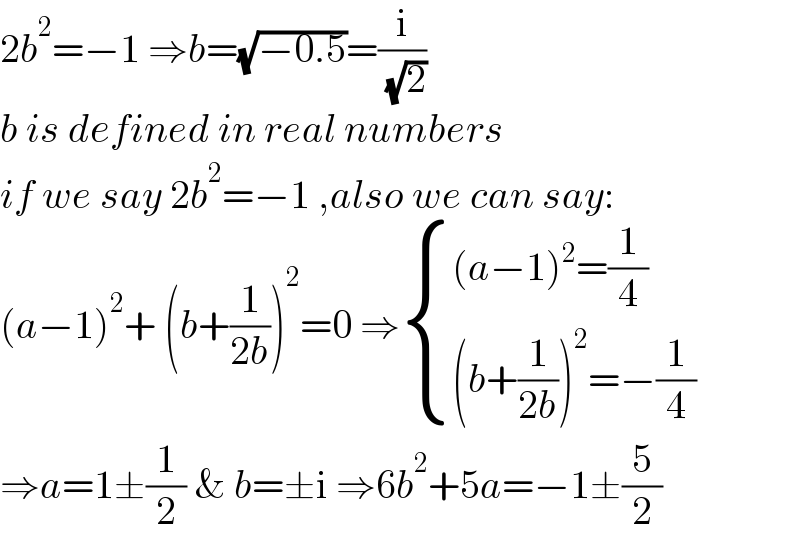
$$\mathrm{2}{b}^{\mathrm{2}} =−\mathrm{1}\:\Rightarrow{b}=\sqrt{−\mathrm{0}.\mathrm{5}}=\frac{\mathrm{i}}{\:\sqrt{\mathrm{2}}}\: \\ $$$${b}\:{is}\:{defined}\:{in}\:{real}\:{numbers} \\ $$$${if}\:{we}\:{say}\:\mathrm{2}{b}^{\mathrm{2}} =−\mathrm{1}\:,{also}\:{we}\:{can}\:{say}: \\ $$$$\left({a}−\mathrm{1}\right)^{\mathrm{2}} +\:\left({b}+\frac{\mathrm{1}}{\mathrm{2}{b}}\right)^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\begin{cases}{\left({a}−\mathrm{1}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}}\\{\left({b}+\frac{\mathrm{1}}{\mathrm{2}{b}}\right)^{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{4}}}\end{cases} \\ $$$$\Rightarrow{a}=\mathrm{1}\pm\frac{\mathrm{1}}{\mathrm{2}}\:\&\:{b}=\pm\mathrm{i}\:\Rightarrow\mathrm{6}{b}^{\mathrm{2}} +\mathrm{5}{a}=−\mathrm{1}\pm\frac{\mathrm{5}}{\mathrm{2}} \\ $$
