Question Number 99877 by I want to learn more last updated on 23/Jun/20

Commented by bobhans last updated on 24/Jun/20
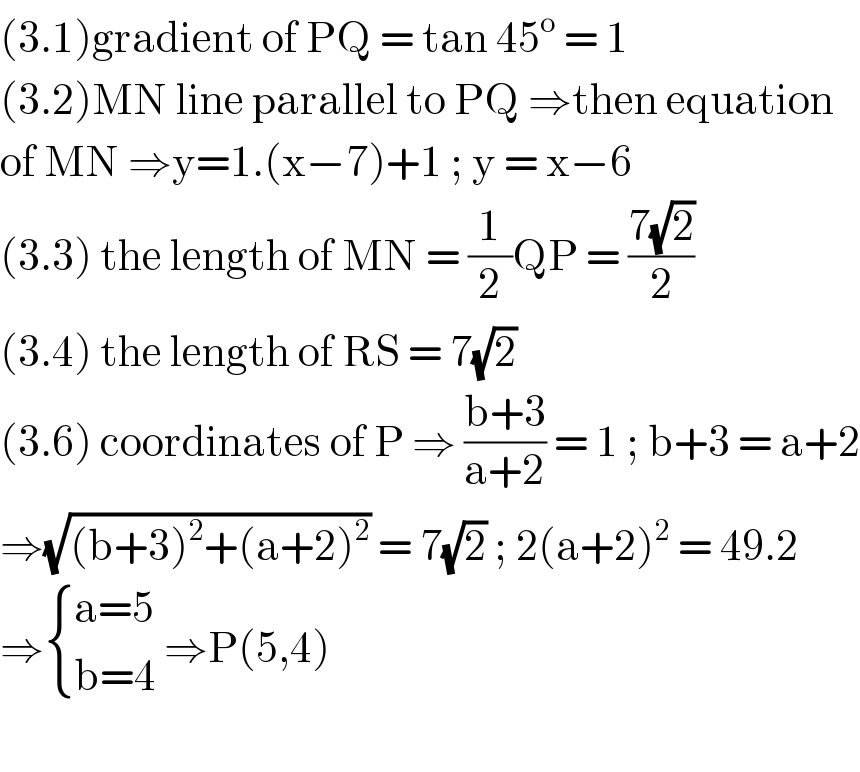
$$\left(\mathrm{3}.\mathrm{1}\right)\mathrm{gradient}\:\mathrm{of}\:\mathrm{PQ}\:=\:\mathrm{tan}\:\mathrm{45}^{\mathrm{o}} \:=\:\mathrm{1} \\ $$$$\left(\mathrm{3}.\mathrm{2}\right)\mathrm{MN}\:\mathrm{line}\:\mathrm{parallel}\:\mathrm{to}\:\mathrm{PQ}\:\Rightarrow\mathrm{then}\:\mathrm{equation} \\ $$$$\mathrm{of}\:\mathrm{MN}\:\Rightarrow\mathrm{y}=\mathrm{1}.\left(\mathrm{x}−\mathrm{7}\right)+\mathrm{1}\:;\:\mathrm{y}\:=\:\mathrm{x}−\mathrm{6}\: \\ $$$$\left(\mathrm{3}.\mathrm{3}\right)\:\mathrm{the}\:\mathrm{length}\:\mathrm{of}\:\mathrm{MN}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{QP}\:=\:\frac{\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\left(\mathrm{3}.\mathrm{4}\right)\:\mathrm{the}\:\mathrm{length}\:\mathrm{of}\:\mathrm{RS}\:=\:\mathrm{7}\sqrt{\mathrm{2}} \\ $$$$\left(\mathrm{3}.\mathrm{6}\right)\:\mathrm{coordinates}\:\mathrm{of}\:\mathrm{P}\:\Rightarrow\:\frac{\mathrm{b}+\mathrm{3}}{\mathrm{a}+\mathrm{2}}\:=\:\mathrm{1}\:;\:\mathrm{b}+\mathrm{3}\:=\:\mathrm{a}+\mathrm{2} \\ $$$$\Rightarrow\sqrt{\left(\mathrm{b}+\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{a}+\mathrm{2}\right)^{\mathrm{2}} }\:=\:\mathrm{7}\sqrt{\mathrm{2}}\:;\:\mathrm{2}\left(\mathrm{a}+\mathrm{2}\right)^{\mathrm{2}} \:=\:\mathrm{49}.\mathrm{2} \\ $$$$\Rightarrow\begin{cases}{\mathrm{a}=\mathrm{5}}\\{\mathrm{b}=\mathrm{4}}\end{cases}\:\Rightarrow\mathrm{P}\left(\mathrm{5},\mathrm{4}\right) \\ $$$$ \\ $$
Commented by bobhans last updated on 24/Jun/20
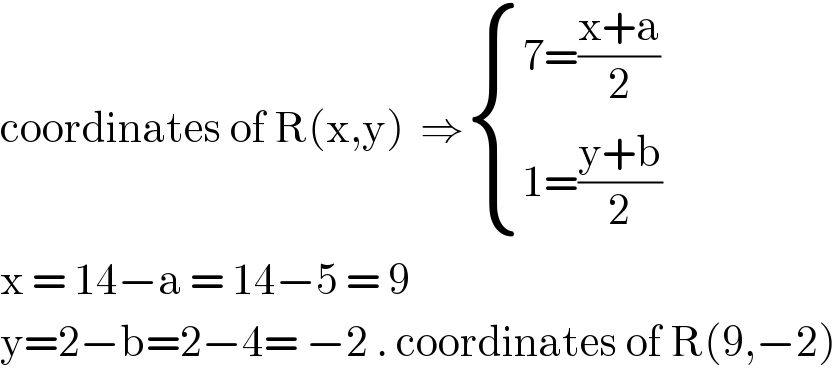
$$\mathrm{coordinates}\:\mathrm{of}\:\mathrm{R}\left(\mathrm{x},\mathrm{y}\right)\:\:\Rightarrow\begin{cases}{\mathrm{7}=\frac{\mathrm{x}+\mathrm{a}}{\mathrm{2}}}\\{\mathrm{1}=\frac{\mathrm{y}+\mathrm{b}}{\mathrm{2}}}\end{cases} \\ $$$$\mathrm{x}\:=\:\mathrm{14}−\mathrm{a}\:=\:\mathrm{14}−\mathrm{5}\:=\:\mathrm{9} \\ $$$$\mathrm{y}=\mathrm{2}−\mathrm{b}=\mathrm{2}−\mathrm{4}=\:−\mathrm{2}\:.\:\mathrm{coordinates}\:\mathrm{of}\:\mathrm{R}\left(\mathrm{9},−\mathrm{2}\right) \\ $$
Commented by I want to learn more last updated on 24/Jun/20
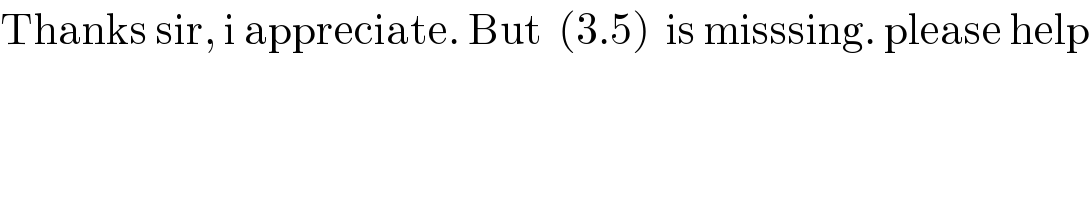
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}.\:\mathrm{But}\:\:\left(\mathrm{3}.\mathrm{5}\right)\:\:\mathrm{is}\:\mathrm{misssing}.\:\mathrm{please}\:\mathrm{help} \\ $$
Commented by bobhans last updated on 24/Jun/20
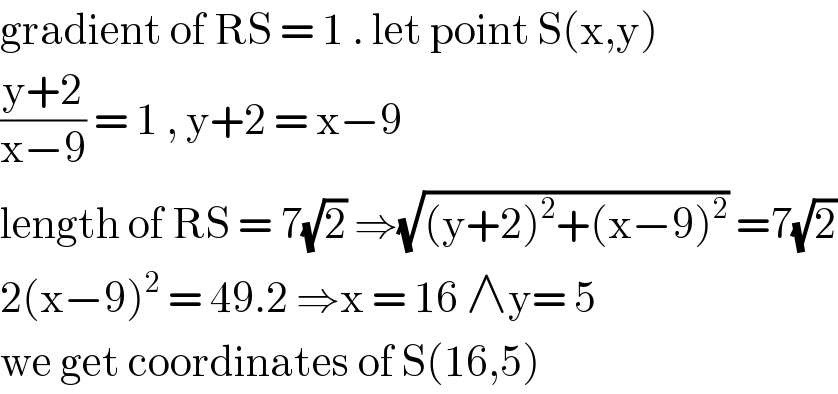
$$\mathrm{gradient}\:\mathrm{of}\:\mathrm{RS}\:=\:\mathrm{1}\:.\:\mathrm{let}\:\mathrm{point}\:\mathrm{S}\left(\mathrm{x},\mathrm{y}\right) \\ $$$$\frac{\mathrm{y}+\mathrm{2}}{\mathrm{x}−\mathrm{9}}\:=\:\mathrm{1}\:,\:\mathrm{y}+\mathrm{2}\:=\:\mathrm{x}−\mathrm{9} \\ $$$$\mathrm{length}\:\mathrm{of}\:\mathrm{RS}\:=\:\mathrm{7}\sqrt{\mathrm{2}}\:\Rightarrow\sqrt{\left(\mathrm{y}+\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{x}−\mathrm{9}\right)^{\mathrm{2}} }\:=\mathrm{7}\sqrt{\mathrm{2}} \\ $$$$\mathrm{2}\left(\mathrm{x}−\mathrm{9}\right)^{\mathrm{2}} \:=\:\mathrm{49}.\mathrm{2}\:\Rightarrow\mathrm{x}\:=\:\mathrm{16}\:\wedge\mathrm{y}=\:\mathrm{5} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{coordinates}\:\mathrm{of}\:\mathrm{S}\left(\mathrm{16},\mathrm{5}\right) \\ $$
Commented by I want to learn more last updated on 24/Jun/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
