Question Number 165576 by mathocean1 last updated on 04/Feb/22
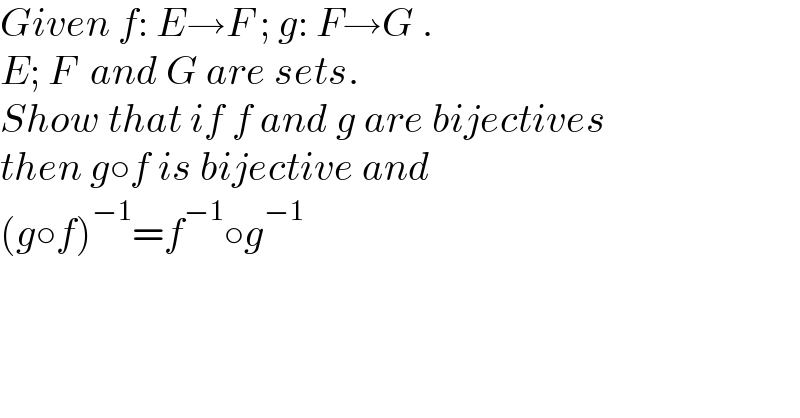
$${Given}\:{f}:\:{E}\rightarrow{F}\:;\:{g}:\:{F}\rightarrow{G}\:. \\ $$$${E};\:{F}\:\:{and}\:{G}\:{are}\:{sets}. \\ $$$${Show}\:{that}\:{if}\:{f}\:{and}\:{g}\:{are}\:{bijectives} \\ $$$${then}\:{g}\circ{f}\:{is}\:{bijective}\:{and}\: \\ $$$$\left({g}\circ{f}\right)^{−\mathrm{1}} ={f}^{−\mathrm{1}} \circ{g}^{−\mathrm{1}} \\ $$
Answered by aleks041103 last updated on 04/Feb/22
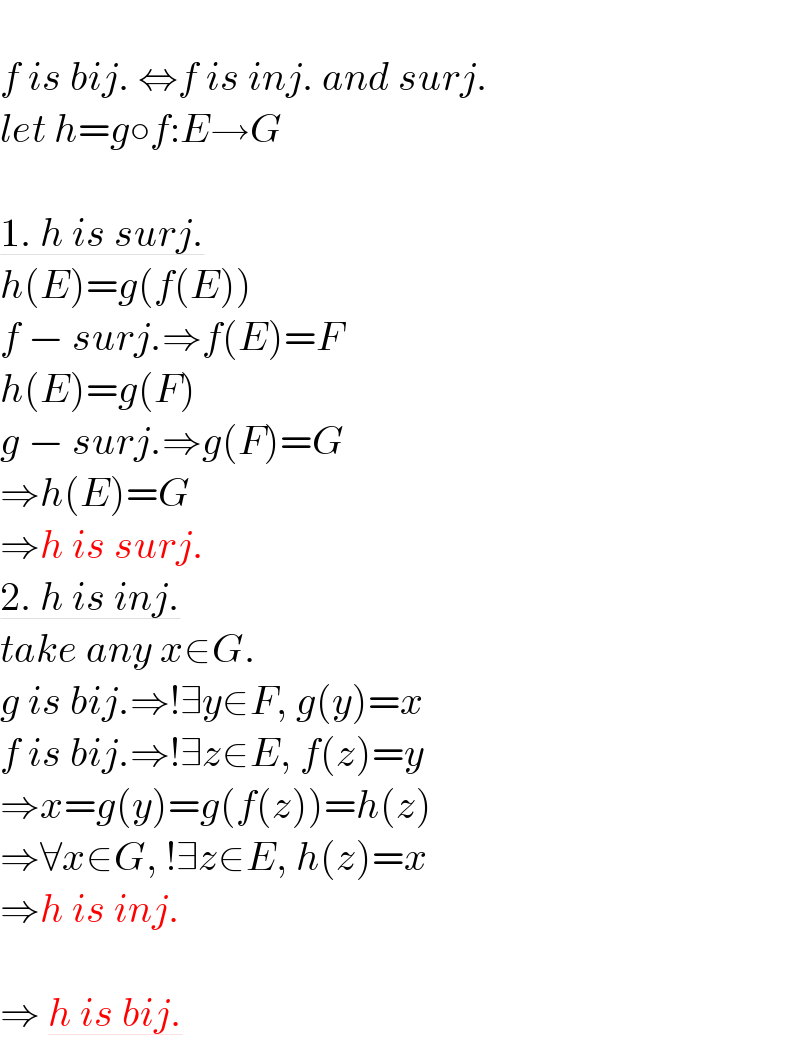
$$ \\ $$$${f}\:{is}\:{bij}.\:\Leftrightarrow{f}\:{is}\:{inj}.\:{and}\:{surj}. \\ $$$${let}\:{h}={g}\circ{f}:{E}\rightarrow{G} \\ $$$$ \\ $$$$\underline{\mathrm{1}.\:{h}\:{is}\:{surj}.} \\ $$$${h}\left({E}\right)={g}\left({f}\left({E}\right)\right) \\ $$$${f}\:−\:{surj}.\Rightarrow{f}\left({E}\right)={F} \\ $$$${h}\left({E}\right)={g}\left({F}\right) \\ $$$${g}\:−\:{surj}.\Rightarrow{g}\left({F}\right)={G} \\ $$$$\Rightarrow{h}\left({E}\right)={G} \\ $$$$\Rightarrow{h}\:{is}\:{surj}. \\ $$$$\underline{\mathrm{2}.\:{h}\:{is}\:{inj}.} \\ $$$${take}\:{any}\:{x}\in{G}. \\ $$$${g}\:{is}\:{bij}.\Rightarrow!\exists{y}\in{F},\:{g}\left({y}\right)={x} \\ $$$${f}\:{is}\:{bij}.\Rightarrow!\exists{z}\in{E},\:{f}\left({z}\right)={y} \\ $$$$\Rightarrow{x}={g}\left({y}\right)={g}\left({f}\left({z}\right)\right)={h}\left({z}\right) \\ $$$$\Rightarrow\forall{x}\in{G},\:!\exists{z}\in{E},\:{h}\left({z}\right)={x} \\ $$$$\Rightarrow{h}\:{is}\:{inj}. \\ $$$$ \\ $$$$\Rightarrow\:\underline{{h}\:{is}\:{bij}.} \\ $$
Answered by aleks041103 last updated on 04/Feb/22
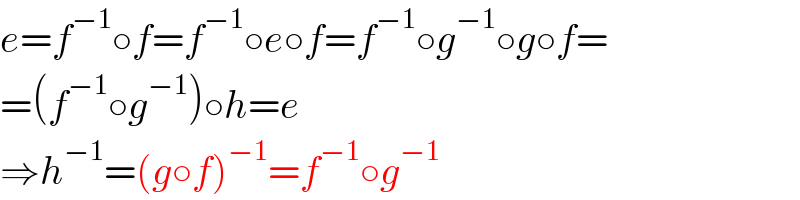
$${e}={f}^{−\mathrm{1}} \circ{f}={f}^{−\mathrm{1}} \circ{e}\circ{f}={f}^{−\mathrm{1}} \circ{g}^{−\mathrm{1}} \circ{g}\circ{f}= \\ $$$$=\left({f}^{−\mathrm{1}} \circ{g}^{−\mathrm{1}} \right)\circ{h}={e} \\ $$$$\Rightarrow{h}^{−\mathrm{1}} =\left({g}\circ{f}\right)^{−\mathrm{1}} ={f}^{−\mathrm{1}} \circ{g}^{−\mathrm{1}} \\ $$
