Question Number 100193 by bobhans last updated on 25/Jun/20
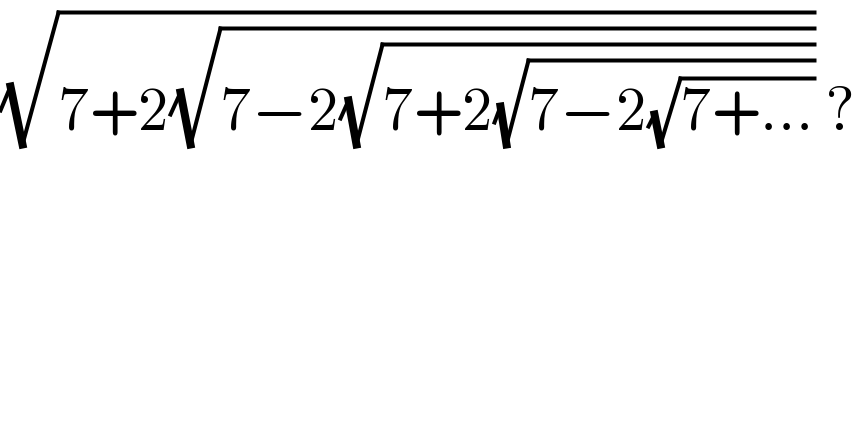
$$\sqrt{\mathrm{7}+\mathrm{2}\sqrt{\mathrm{7}−\mathrm{2}\sqrt{\mathrm{7}+\mathrm{2}\sqrt{\mathrm{7}−\mathrm{2}\sqrt{\mathrm{7}+…}}}}}\:? \\ $$
Commented by bobhans last updated on 25/Jun/20
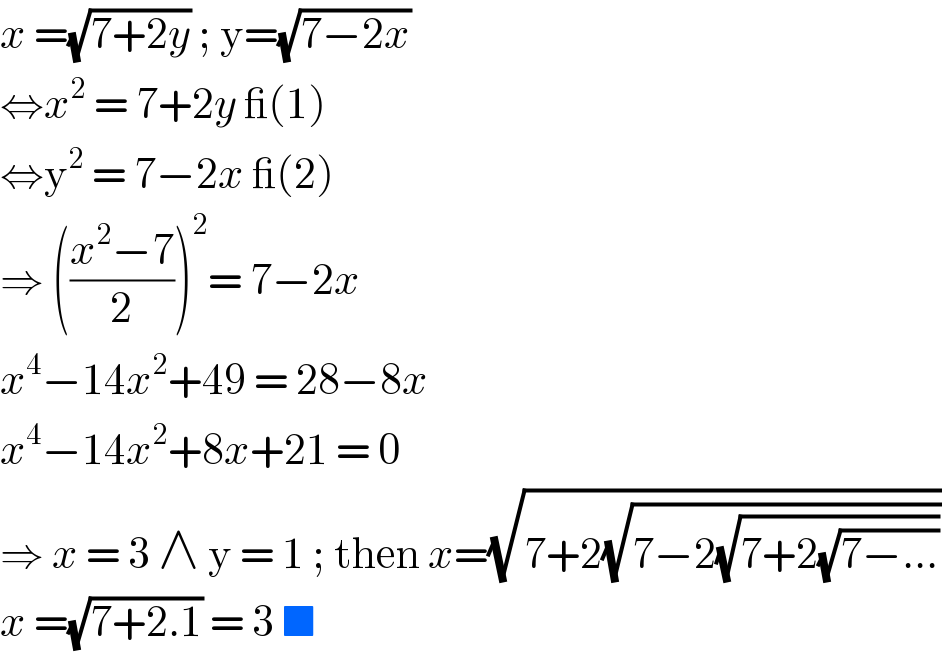
$${x}\:=\sqrt{\mathrm{7}+\mathrm{2}{y}}\:;\:\mathrm{y}=\sqrt{\mathrm{7}−\mathrm{2}{x}} \\ $$$$\Leftrightarrow{x}^{\mathrm{2}} \:=\:\mathrm{7}+\mathrm{2}{y}\:\_\left(\mathrm{1}\right) \\ $$$$\Leftrightarrow\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{7}−\mathrm{2}{x}\:\_\left(\mathrm{2}\right) \\ $$$$\Rightarrow\:\left(\frac{{x}^{\mathrm{2}} −\mathrm{7}}{\mathrm{2}}\right)^{\mathrm{2}} =\:\mathrm{7}−\mathrm{2}{x}\: \\ $$$${x}^{\mathrm{4}} −\mathrm{14}{x}^{\mathrm{2}} +\mathrm{49}\:=\:\mathrm{28}−\mathrm{8}{x} \\ $$$${x}^{\mathrm{4}} −\mathrm{14}{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{21}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{x}\:=\:\mathrm{3}\:\wedge\:\mathrm{y}\:=\:\mathrm{1}\:;\:\mathrm{then}\:{x}=\sqrt{\mathrm{7}+\mathrm{2}\sqrt{\mathrm{7}−\mathrm{2}\sqrt{\mathrm{7}+\mathrm{2}\sqrt{\mathrm{7}−…}}}} \\ $$$${x}\:=\sqrt{\mathrm{7}+\mathrm{2}.\mathrm{1}}\:=\:\mathrm{3}\:\blacksquare \\ $$
Commented by Dwaipayan Shikari last updated on 25/Jun/20

$${Yes}\:{it}\:{is}\:\mathrm{3} \\ $$
Commented by Dwaipayan Shikari last updated on 25/Jun/20

$${I}\:{also}\:{did}\:{this} \\ $$
Answered by Dwaipayan Shikari last updated on 25/Jun/20
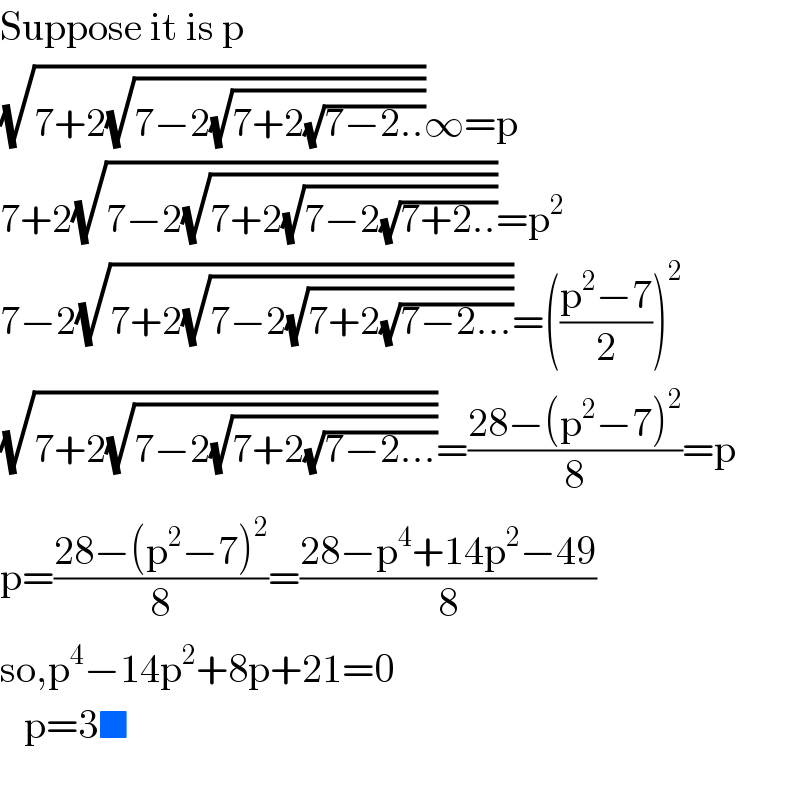
$$\mathrm{Suppose}\:\mathrm{it}\:\mathrm{is}\:\mathrm{p} \\ $$$$\sqrt{\mathrm{7}+\mathrm{2}\sqrt{\mathrm{7}−\mathrm{2}\sqrt{\mathrm{7}+\mathrm{2}\sqrt{\mathrm{7}−\mathrm{2}..}}}}\infty=\mathrm{p} \\ $$$$\mathrm{7}+\mathrm{2}\sqrt{\mathrm{7}−\mathrm{2}\sqrt{\mathrm{7}+\mathrm{2}\sqrt{\mathrm{7}−\mathrm{2}\sqrt{\mathrm{7}+\mathrm{2}..}}}}=\mathrm{p}^{\mathrm{2}} \\ $$$$\mathrm{7}−\mathrm{2}\sqrt{\mathrm{7}+\mathrm{2}\sqrt{\mathrm{7}−\mathrm{2}\sqrt{\mathrm{7}+\mathrm{2}\sqrt{\mathrm{7}−\mathrm{2}…}}}}=\left(\frac{\mathrm{p}^{\mathrm{2}} −\mathrm{7}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\sqrt{\mathrm{7}+\mathrm{2}\sqrt{\mathrm{7}−\mathrm{2}\sqrt{\mathrm{7}+\mathrm{2}\sqrt{\mathrm{7}−\mathrm{2}…}}}}=\frac{\mathrm{28}−\left(\mathrm{p}^{\mathrm{2}} −\mathrm{7}\right)^{\mathrm{2}} }{\mathrm{8}}=\mathrm{p} \\ $$$$\mathrm{p}=\frac{\mathrm{28}−\left(\mathrm{p}^{\mathrm{2}} −\mathrm{7}\right)^{\mathrm{2}} }{\mathrm{8}}=\frac{\mathrm{28}−\mathrm{p}^{\mathrm{4}} +\mathrm{14p}^{\mathrm{2}} −\mathrm{49}}{\mathrm{8}} \\ $$$$\mathrm{so},\mathrm{p}^{\mathrm{4}} −\mathrm{14p}^{\mathrm{2}} +\mathrm{8p}+\mathrm{21}=\mathrm{0} \\ $$$$\:\:\:\mathrm{p}=\mathrm{3}\blacksquare \\ $$$$ \\ $$
