Question Number 289 by 123456 last updated on 25/Jan/15
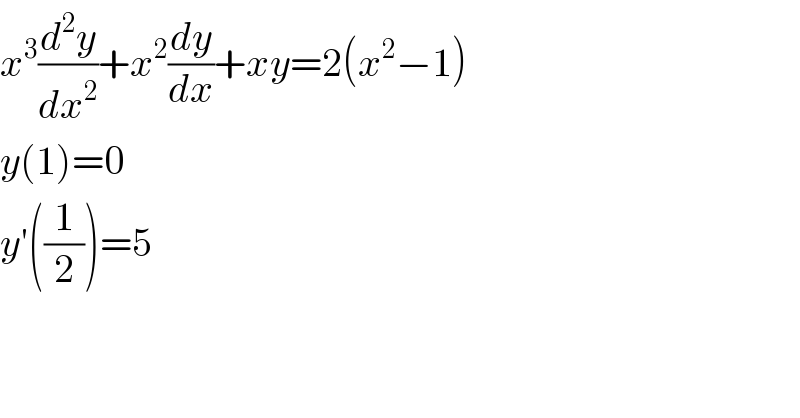
$${x}^{\mathrm{3}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+{x}^{\mathrm{2}} \frac{{dy}}{{dx}}+{xy}=\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$${y}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$${y}'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{5} \\ $$
Answered by prakash jain last updated on 18/Dec/14
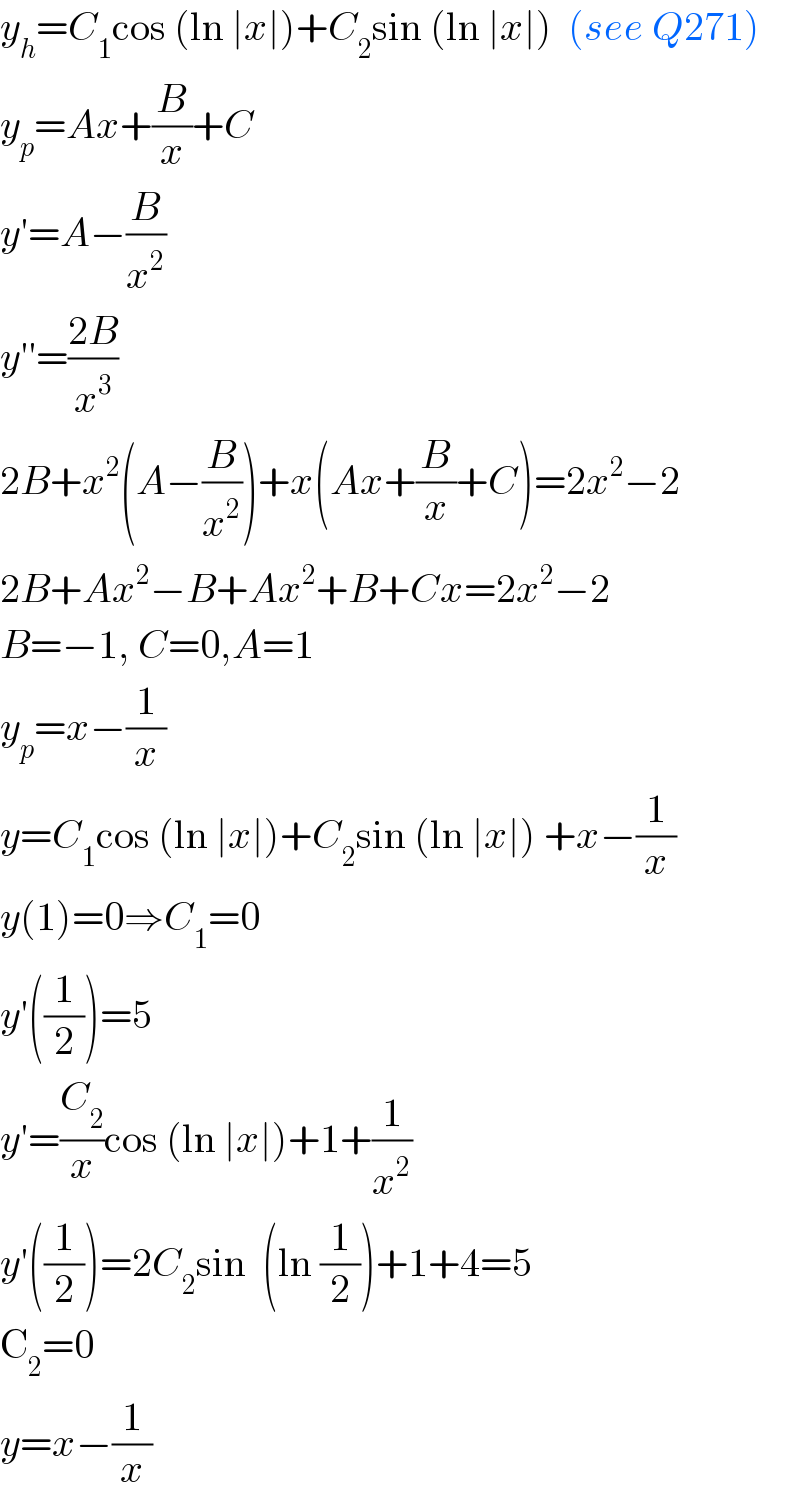
$${y}_{{h}} ={C}_{\mathrm{1}} \mathrm{cos}\:\left(\mathrm{ln}\:\mid{x}\mid\right)+{C}_{\mathrm{2}} \mathrm{sin}\:\left(\mathrm{ln}\:\mid{x}\mid\right)\:\:\left({see}\:{Q}\mathrm{271}\right) \\ $$$${y}_{{p}} ={Ax}+\frac{{B}}{{x}}+{C} \\ $$$${y}'={A}−\frac{{B}}{{x}^{\mathrm{2}} } \\ $$$${y}''=\frac{\mathrm{2}{B}}{{x}^{\mathrm{3}} } \\ $$$$\mathrm{2}{B}+{x}^{\mathrm{2}} \left({A}−\frac{{B}}{{x}^{\mathrm{2}} }\right)+{x}\left({Ax}+\frac{{B}}{{x}}+{C}\right)=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2} \\ $$$$\mathrm{2}{B}+{Ax}^{\mathrm{2}} −{B}+{Ax}^{\mathrm{2}} +{B}+{Cx}=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2} \\ $$$${B}=−\mathrm{1},\:{C}=\mathrm{0},{A}=\mathrm{1} \\ $$$${y}_{{p}} ={x}−\frac{\mathrm{1}}{{x}} \\ $$$${y}={C}_{\mathrm{1}} \mathrm{cos}\:\left(\mathrm{ln}\:\mid{x}\mid\right)+{C}_{\mathrm{2}} \mathrm{sin}\:\left(\mathrm{ln}\:\mid{x}\mid\right)\:+{x}−\frac{\mathrm{1}}{{x}} \\ $$$${y}\left(\mathrm{1}\right)=\mathrm{0}\Rightarrow{C}_{\mathrm{1}} =\mathrm{0} \\ $$$${y}'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{5} \\ $$$${y}'=\frac{{C}_{\mathrm{2}} }{{x}}\mathrm{cos}\:\left(\mathrm{ln}\:\mid{x}\mid\right)+\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$${y}'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2}{C}_{\mathrm{2}} \mathrm{sin}\:\:\left(\mathrm{ln}\:\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{1}+\mathrm{4}=\mathrm{5} \\ $$$$\mathrm{C}_{\mathrm{2}} =\mathrm{0} \\ $$$${y}={x}−\frac{\mathrm{1}}{{x}} \\ $$
