Question Number 134428 by liberty last updated on 03/Mar/21

$$\mathrm{In}\:\mathrm{a}\:\mathrm{cube}\:\mathrm{ABCD}.\mathrm{EFGH}\:\mathrm{with}\:\mathrm{a} \\ $$$$\mathrm{side}\:\mathrm{length}\:\mathrm{of}\:\mathrm{4}\:\mathrm{cm}.\:\mathrm{Point}\:\mathrm{Q}\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{middle}\:\mathrm{of}\:\mathrm{line}\:\mathrm{AE}\:\mathrm{and}\:\mathrm{point}\:\mathrm{P} \\ $$$$\mathrm{lies}\:\mathrm{on}\:\mathrm{the}\:\mathrm{extension}\:\mathrm{of}\:\mathrm{line}\:\mathrm{AB} \\ $$$$\mathrm{so}\:\mathrm{that}\:\mathrm{BP}\::\:\mathrm{AB}\:=\:\mathrm{1}\::\:\mathrm{2}.\:\mathrm{If}\:\theta\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{angle}\:\mathrm{between}\:\mathrm{the}\:\mathrm{QG}\:\mathrm{line}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{PQH}\:\mathrm{plane}\:,\:\mathrm{then}\:\mathrm{sin}\:\theta\:=?\: \\ $$
Answered by EDWIN88 last updated on 03/Mar/21
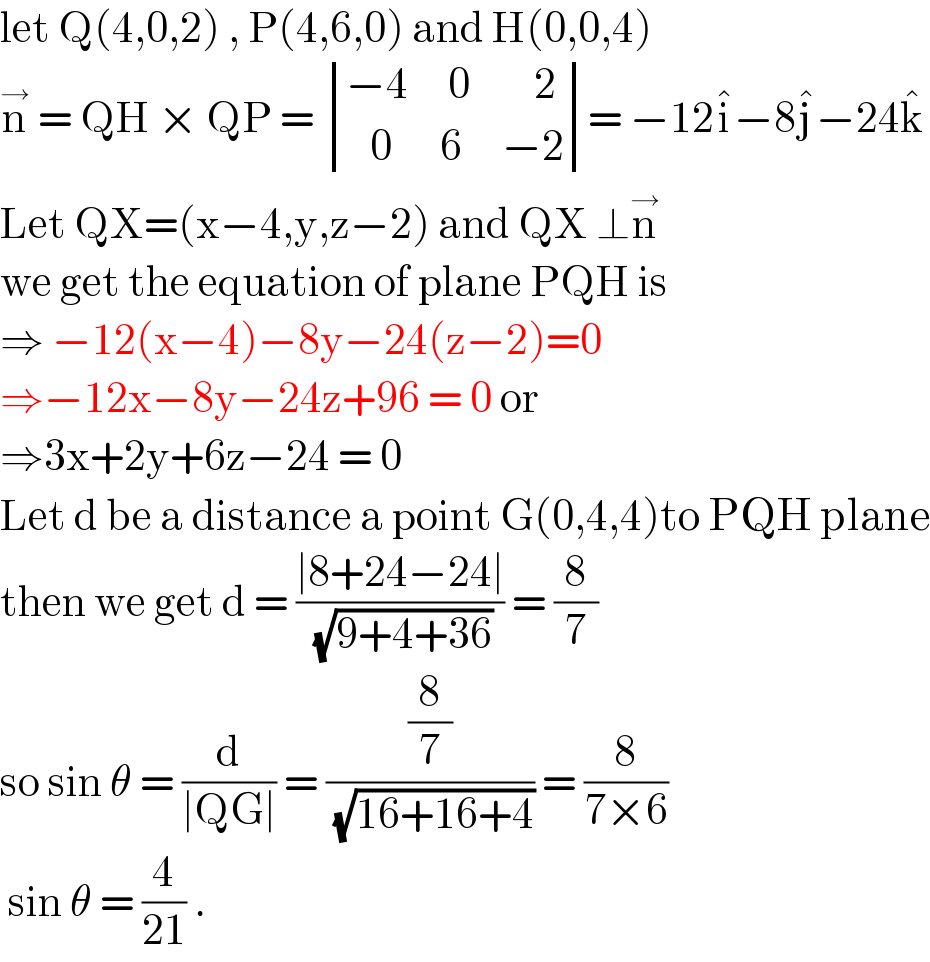
$$\mathrm{let}\:\mathrm{Q}\left(\mathrm{4},\mathrm{0},\mathrm{2}\right)\:,\:\mathrm{P}\left(\mathrm{4},\mathrm{6},\mathrm{0}\right)\:\mathrm{and}\:\mathrm{H}\left(\mathrm{0},\mathrm{0},\mathrm{4}\right) \\ $$$$\overset{\rightarrow} {\mathrm{n}}\:=\:\mathrm{QH}\:×\:\mathrm{QP}\:=\:\begin{vmatrix}{−\mathrm{4}\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{2}}\\{\:\:\:\mathrm{0}\:\:\:\:\:\:\mathrm{6}\:\:\:\:\:−\mathrm{2}}\end{vmatrix}=\:−\mathrm{12}\hat {\mathrm{i}}−\mathrm{8}\hat {\mathrm{j}}−\mathrm{24}\hat {\mathrm{k}} \\ $$$$\mathrm{Let}\:\mathrm{QX}=\left(\mathrm{x}−\mathrm{4},\mathrm{y},\mathrm{z}−\mathrm{2}\right)\:\mathrm{and}\:\mathrm{QX}\:\bot\overset{\rightarrow} {\mathrm{n}} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{plane}\:\mathrm{PQH}\:\mathrm{is} \\ $$$$\Rightarrow\:−\mathrm{12}\left(\mathrm{x}−\mathrm{4}\right)−\mathrm{8y}−\mathrm{24}\left(\mathrm{z}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow−\mathrm{12x}−\mathrm{8y}−\mathrm{24z}+\mathrm{96}\:=\:\mathrm{0}\:\mathrm{or}\: \\ $$$$\Rightarrow\mathrm{3x}+\mathrm{2y}+\mathrm{6z}−\mathrm{24}\:=\:\mathrm{0} \\ $$$$\mathrm{Let}\:\mathrm{d}\:\mathrm{be}\:\mathrm{a}\:\mathrm{distance}\:\mathrm{a}\:\mathrm{point}\:\mathrm{G}\left(\mathrm{0},\mathrm{4},\mathrm{4}\right)\mathrm{to}\:\mathrm{PQH}\:\mathrm{plane} \\ $$$$\mathrm{then}\:\mathrm{we}\:\mathrm{get}\:\mathrm{d}\:=\:\frac{\mid\mathrm{8}+\mathrm{24}−\mathrm{24}\mid}{\:\sqrt{\mathrm{9}+\mathrm{4}+\mathrm{36}}}\:=\:\frac{\mathrm{8}}{\mathrm{7}} \\ $$$$\mathrm{so}\:\mathrm{sin}\:\theta\:=\:\frac{\mathrm{d}}{\mid\mathrm{QG}\mid}\:=\:\frac{\frac{\mathrm{8}}{\mathrm{7}}}{\:\sqrt{\mathrm{16}+\mathrm{16}+\mathrm{4}}}\:=\:\frac{\mathrm{8}}{\mathrm{7}×\mathrm{6}} \\ $$$$\:\mathrm{sin}\:\theta\:=\:\frac{\mathrm{4}}{\mathrm{21}}\:.\: \\ $$
Answered by mr W last updated on 03/Mar/21
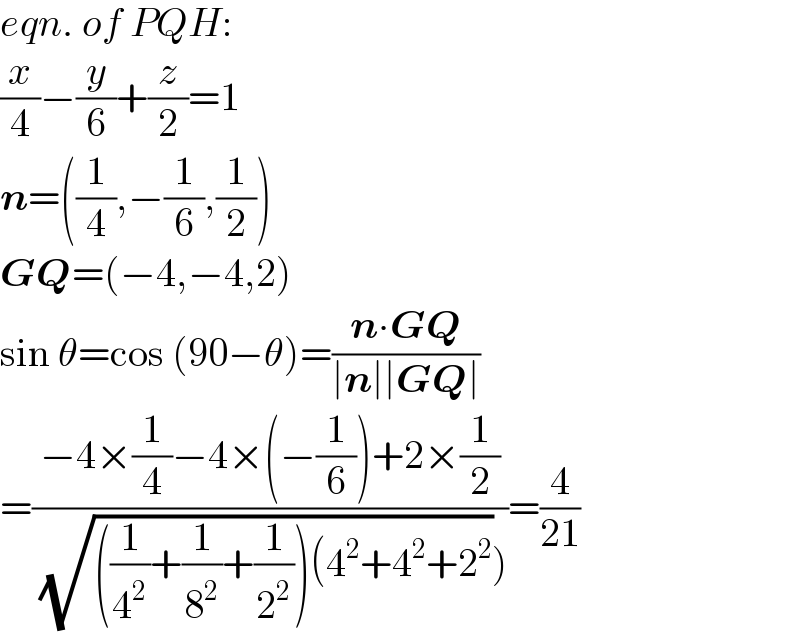
$${eqn}.\:{of}\:{PQH}: \\ $$$$\frac{{x}}{\mathrm{4}}−\frac{{y}}{\mathrm{6}}+\frac{{z}}{\mathrm{2}}=\mathrm{1} \\ $$$$\boldsymbol{{n}}=\left(\frac{\mathrm{1}}{\mathrm{4}},−\frac{\mathrm{1}}{\mathrm{6}},\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\boldsymbol{{GQ}}=\left(−\mathrm{4},−\mathrm{4},\mathrm{2}\right) \\ $$$$\mathrm{sin}\:\theta=\mathrm{cos}\:\left(\mathrm{90}−\theta\right)=\frac{\boldsymbol{{n}}\centerdot\boldsymbol{{GQ}}}{\mid\boldsymbol{{n}}\mid\mid\boldsymbol{{GQ}}\mid} \\ $$$$=\frac{−\mathrm{4}×\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{4}×\left(−\frac{\mathrm{1}}{\mathrm{6}}\right)+\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}}{\left.\:\sqrt{\left(\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{8}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)\left(\mathrm{4}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} \right.}\right)}=\frac{\mathrm{4}}{\mathrm{21}} \\ $$
