Menu Close

Advanced-calculus-prove-that-P-n-1-1-1-n-4-sin-pi-sinh-pi-pi-2-

Tinku Tara 0 Comments
Pin




Question Number 134435 by mnjuly1970 last updated on 03/Mar/21
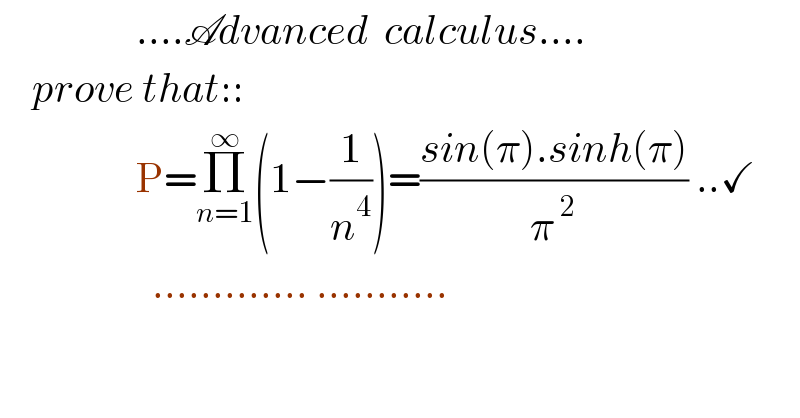
....Advanced calculus.... prove that:: P=Π_(n=1) ^∞ (1−(1/n^4 ))=((sin(π).sinh(π))/π^( 2) ) ..✓ ............. ...........
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\mathscr{A}{dvanced}\:\:{calculus}…. \\ $$$$\:\:\:\:{prove}\:{that}:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{P}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{4}} }\right)=\frac{{sin}\left(\pi\right).{sinh}\left(\pi\right)}{\pi^{\:\mathrm{2}} }\:..\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:………….\:……….. \\ $$
Answered by Dwaipayan Shikari last updated on 03/Mar/21
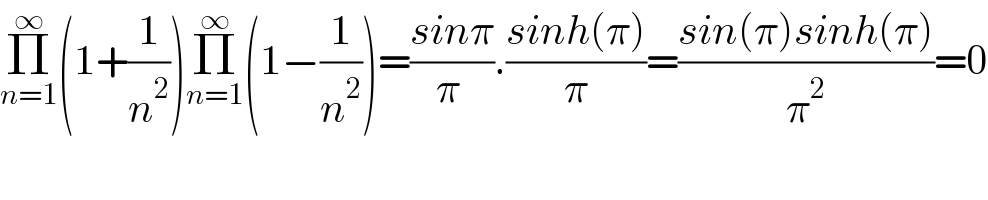
Π_(n=1) ^∞ (1+(1/n^2 ))Π_(n=1) ^∞ (1−(1/n^2 ))=((sinπ)/(π )).((sinh(π))/π)=((sin(π)sinh(π))/π^2 )=0
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)=\frac{{sin}\pi}{\pi\:}.\frac{{sinh}\left(\pi\right)}{\pi}=\frac{{sin}\left(\pi\right){sinh}\left(\pi\right)}{\pi^{\mathrm{2}} }=\mathrm{0} \\ $$
Commented by mnjuly1970 last updated on 03/Mar/21
tayeballah sir payan...
$${tayeballah}\:{sir}\:{payan}… \\ $$
Answered by mnjuly1970 last updated on 03/Mar/21
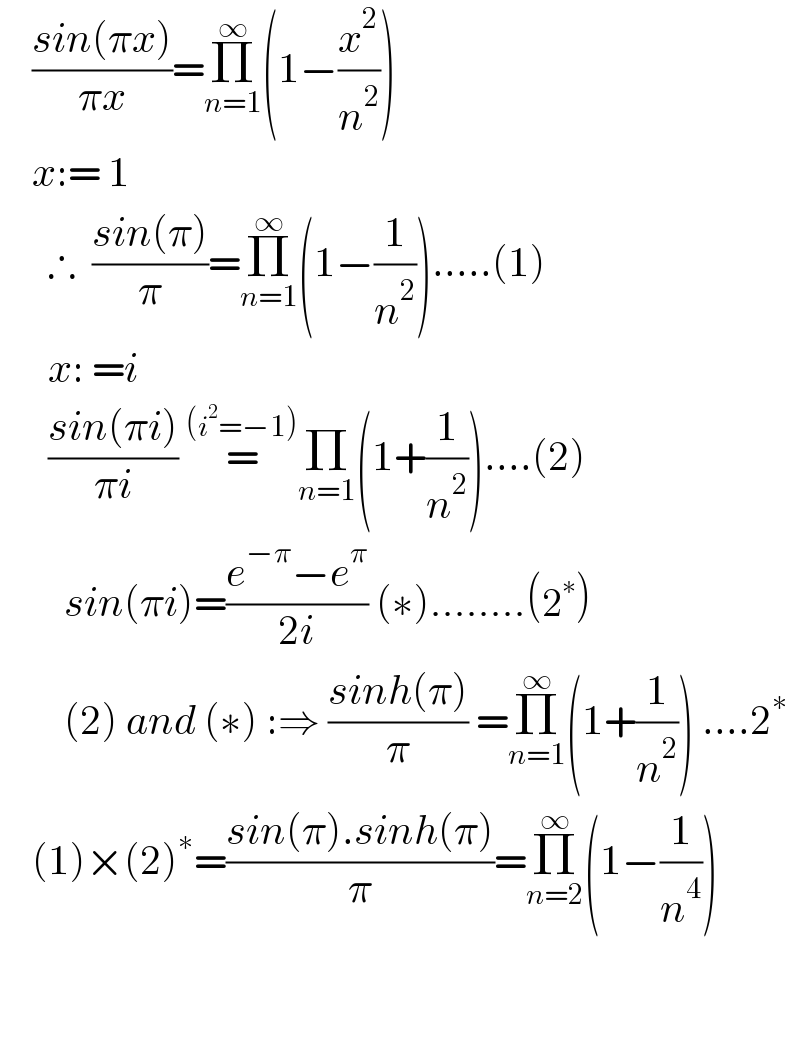
((sin(πx))/(πx))=Π_(n=1) ^∞ (1−(x^2 /n^2 )) x:= 1 ∴ ((sin(π))/π)=Π_(n=1) ^∞ (1−(1/n^2 )).....(1) x: =i ((sin(πi))/(πi)) =^((i^2 =−1)) Π_(n=1) (1+(1/n^2 ))....(2) sin(πi)=((e^(−π) −e^π )/(2i)) (∗)........(2^∗ ) (2) and (∗) :⇒ ((sinh(π))/π) =Π_(n=1) ^∞ (1+(1/n^2 )) ....2^∗ (1)×(2)^∗ =((sin(π).sinh(π))/π)=Π_(n=2) ^∞ (1−(1/n^4 ))
$$\:\:\:\:\frac{{sin}\left(\pi{x}\right)}{\pi{x}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:{x}:=\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\therefore\:\:\frac{{sin}\left(\pi\right)}{\pi}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)…..\left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:{x}:\:={i} \\ $$$$\:\:\:\:\:\:\frac{{sin}\left(\pi{i}\right)}{\pi{i}}\:\overset{\left({i}^{\mathrm{2}} =−\mathrm{1}\right)} {=}\underset{{n}=\mathrm{1}} {\prod}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)….\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:{sin}\left(\pi{i}\right)=\frac{{e}^{−\pi} −{e}^{\pi} }{\mathrm{2}{i}}\:\left(\ast\right)……..\left(\mathrm{2}^{\ast} \right) \\ $$$$\:\:\:\:\:\:\:\:\left(\mathrm{2}\right)\:{and}\:\left(\ast\right)\::\Rightarrow\:\frac{{sinh}\left(\pi\right)}{\pi}\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\:….\mathrm{2}^{\ast} \\ $$$$\:\:\:\:\left(\mathrm{1}\right)×\left(\mathrm{2}\right)^{\ast} =\frac{{sin}\left(\pi\right).{sinh}\left(\pi\right)}{\pi}=\underset{{n}=\mathrm{2}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{4}} }\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *