Question Number 100385 by bobhans last updated on 26/Jun/20

$$\mathrm{find}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{set}\:\mathrm{of}\:\mathrm{inequality} \\ $$$$\frac{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{9}\right)\sqrt{\mathrm{x}+\mathrm{2}}}{\mathrm{x}+\sqrt{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} }}\:\leqslant\:\mathrm{0} \\ $$
Commented by bobhans last updated on 26/Jun/20
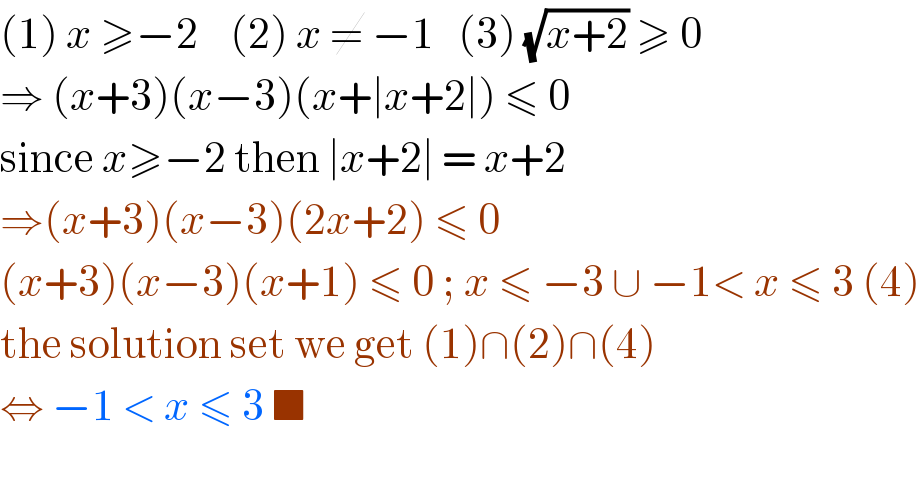
$$\left(\mathrm{1}\right)\:{x}\:\geqslant−\mathrm{2}\:\:\:\:\left(\mathrm{2}\right)\:{x}\:\neq\:−\mathrm{1}\:\:\:\left(\mathrm{3}\right)\:\sqrt{{x}+\mathrm{2}}\:\geqslant\:\mathrm{0} \\ $$$$\Rightarrow\:\left({x}+\mathrm{3}\right)\left({x}−\mathrm{3}\right)\left({x}+\mid{x}+\mathrm{2}\mid\right)\:\leqslant\:\mathrm{0} \\ $$$$\mathrm{since}\:{x}\geqslant−\mathrm{2}\:\mathrm{then}\:\mid{x}+\mathrm{2}\mid\:=\:{x}+\mathrm{2} \\ $$$$\Rightarrow\left({x}+\mathrm{3}\right)\left({x}−\mathrm{3}\right)\left(\mathrm{2}{x}+\mathrm{2}\right)\:\leqslant\:\mathrm{0} \\ $$$$\left({x}+\mathrm{3}\right)\left({x}−\mathrm{3}\right)\left({x}+\mathrm{1}\right)\:\leqslant\:\mathrm{0}\:;\:{x}\:\leqslant\:−\mathrm{3}\:\cup\:−\mathrm{1}<\:{x}\:\leqslant\:\mathrm{3}\:\left(\mathrm{4}\right) \\ $$$$\mathrm{the}\:\mathrm{solution}\:\mathrm{set}\:\mathrm{we}\:\mathrm{get}\:\left(\mathrm{1}\right)\cap\left(\mathrm{2}\right)\cap\left(\mathrm{4}\right) \\ $$$$\Leftrightarrow\:−\mathrm{1}\:<\:{x}\:\leqslant\:\mathrm{3}\:\blacksquare \\ $$$$ \\ $$
Commented by bemath last updated on 26/Jun/20

$$\mathrm{cooll}\: \\ $$$$ \\ $$
Answered by MJS last updated on 26/Jun/20
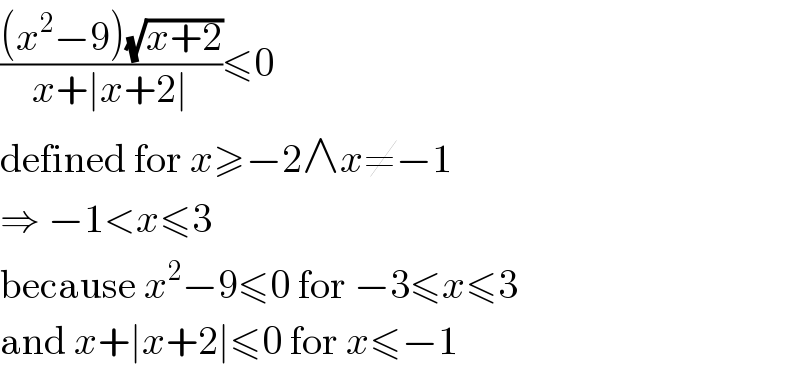
$$\frac{\left({x}^{\mathrm{2}} −\mathrm{9}\right)\sqrt{{x}+\mathrm{2}}}{{x}+\mid{x}+\mathrm{2}\mid}\leqslant\mathrm{0} \\ $$$$\mathrm{defined}\:\mathrm{for}\:{x}\geqslant−\mathrm{2}\wedge{x}\neq−\mathrm{1} \\ $$$$\Rightarrow\:−\mathrm{1}<{x}\leqslant\mathrm{3} \\ $$$$\mathrm{because}\:{x}^{\mathrm{2}} −\mathrm{9}\leqslant\mathrm{0}\:\mathrm{for}\:−\mathrm{3}\leqslant{x}\leqslant\mathrm{3} \\ $$$$\mathrm{and}\:{x}+\mid{x}+\mathrm{2}\mid\leqslant\mathrm{0}\:\mathrm{for}\:{x}\leqslant−\mathrm{1} \\ $$
Commented by bemath last updated on 26/Jun/20
$$\mathrm{great}\:\mathrm{prof}.\:\mathrm{thank}\:\mathrm{much} \\ $$
