Question Number 34988 by ajfour last updated on 14/May/18
Commented by ajfour last updated on 14/May/18

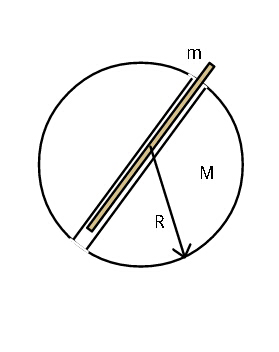
$${If}\:{a}\:{tunnel}\:{is}\:{dug}\:{across}\:{a} \\ $$$${diameter}\:{of}\:{Earth}\:{and}\:{a}\:{rod} \\ $$$${of}\:{mass}\:{m}\:{free}\:{to}\:{oscillate} \\ $$$${about}\:{this}\:{tunnel}\:{is}\:{displaced} \\ $$$${slightly}\:{and}\:{released},\:{find}\:{the} \\ $$$${time}\:{period}\:{of}\:{small}\:{oscillations}. \\ $$
Answered by ajfour last updated on 14/May/18
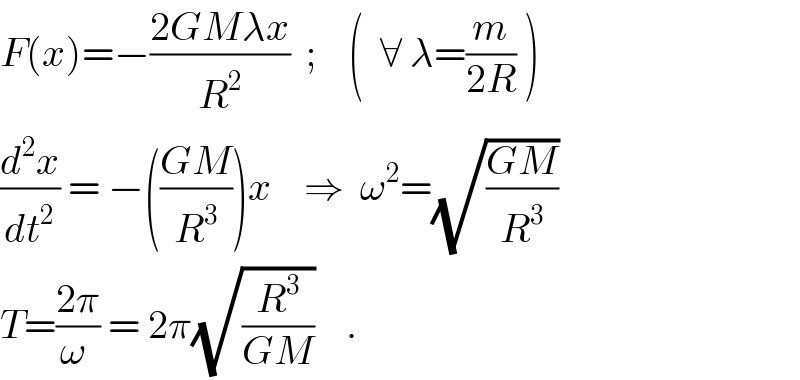
$${F}\left({x}\right)=−\frac{\mathrm{2}{GM}\lambda{x}}{{R}^{\mathrm{2}} }\:\:;\:\:\:\:\left(\:\:\forall\:\lambda=\frac{{m}}{\mathrm{2}{R}}\:\right) \\ $$$$\frac{{d}^{\mathrm{2}} {x}}{{dt}^{\mathrm{2}} }\:=\:−\left(\frac{{GM}}{{R}^{\mathrm{3}} }\right){x}\:\:\:\:\Rightarrow\:\:\omega^{\mathrm{2}} =\sqrt{\frac{{GM}}{{R}^{\mathrm{3}} }}\: \\ $$$${T}=\frac{\mathrm{2}\pi}{\omega\:}\:=\:\mathrm{2}\pi\sqrt{\frac{{R}^{\mathrm{3}} }{{GM}}}\:\:\:\:. \\ $$
