Question Number 35054 by math khazana by abdo last updated on 14/May/18
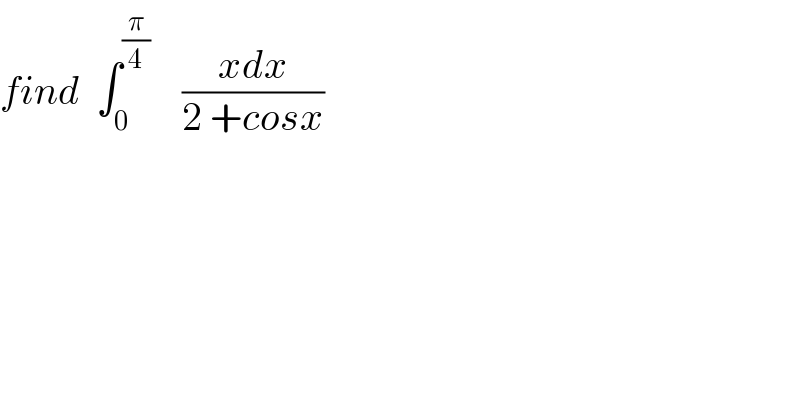
$${find}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{{xdx}}{\mathrm{2}\:+{cosx}} \\ $$
Commented by prof Abdo imad last updated on 16/May/18
![changement tan((x/2))=t give I = ∫_0 ^((√2) −1) ((2arctant)/(2+ ((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) = 4 ∫_0 ^((√2) −1) ((arctant)/(2 +2t^2 +1−t^2 ))dt =4 ∫_0 ^((√2) −1) ((arctan(t))/(3+t^2 )) dt =_(t=(√3)u) 4 ∫_0 ^(((√2)−1)/3) ((arctan((√3)u))/(3(1+u^2 ))) (√3) du =((4(√3))/3) ∫_0 ^(((√2) −1)/3) ((arctan((√3)u))/(1+u^2 ))du by parts ∫_0 ^(((√2)−1)/3) ((arctan((√3)u))/(1+u^2 ))du = [arctan(u)arctan((√3)u)]_0 ^(((√2)−1)/3) −(√3)∫_0 ^(((√2) −1)/3) ((arctan(u))/(1+3u^2 ))du =arctan((((√2) −1)/3))arctan((√3)(((√2) −1)/3)) −(√3) ∫_0 ^(((√2)−1)/3) ((arctan(u))/(1+3u^2 )) du....be continued...](https://www.tinkutara.com/question/Q35185.png)
$${changement}\:\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give} \\ $$$${I}\:\:=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:\:\:\:\frac{\mathrm{2}{arctant}}{\mathrm{2}+\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\mathrm{4}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:\:\:\frac{{arctant}}{\mathrm{2}\:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}−{t}^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:\:\:\:\:\frac{{arctan}\left({t}\right)}{\mathrm{3}+{t}^{\mathrm{2}} }\:{dt} \\ $$$$=_{{t}=\sqrt{\mathrm{3}}{u}} \:\mathrm{4}\:\:\int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{3}}} \:\:\:\:\:\frac{{arctan}\left(\sqrt{\mathrm{3}}{u}\right)}{\mathrm{3}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:\sqrt{\mathrm{3}}\:{du} \\ $$$$=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{2}}\:−\mathrm{1}}{\mathrm{3}}} \:\:\:\:\:\:\frac{{arctan}\left(\sqrt{\mathrm{3}}{u}\right)}{\mathrm{1}+{u}^{\mathrm{2}} }{du}\:\:{by}\:{parts} \\ $$$$\int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{3}}} \:\:\:\:\frac{{arctan}\left(\sqrt{\mathrm{3}}{u}\right)}{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$=\:\left[{arctan}\left({u}\right){arctan}\left(\sqrt{\mathrm{3}}{u}\right)\right]_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{3}}} \:−\sqrt{\mathrm{3}}\int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{2}}\:−\mathrm{1}}{\mathrm{3}}} \:\frac{{arctan}\left({u}\right)}{\mathrm{1}+\mathrm{3}{u}^{\mathrm{2}} }{du} \\ $$$$={arctan}\left(\frac{\sqrt{\mathrm{2}}\:−\mathrm{1}}{\mathrm{3}}\right){arctan}\left(\sqrt{\mathrm{3}}\frac{\sqrt{\mathrm{2}}\:−\mathrm{1}}{\mathrm{3}}\right) \\ $$$$−\sqrt{\mathrm{3}}\:\int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{3}}} \:\:\:\:\:\frac{{arctan}\left({u}\right)}{\mathrm{1}+\mathrm{3}{u}^{\mathrm{2}} }\:{du}….{be}\:{continued}… \\ $$$$ \\ $$
