Question Number 35101 by ajfour last updated on 15/May/18

$${Find}\:{volume}\:{enclosed}\:{by} \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }+\frac{{z}^{\mathrm{2}} }{{c}^{\mathrm{2}} }=\mathrm{1}\:\:. \\ $$
Commented by behi83417@gmail.com last updated on 15/May/18
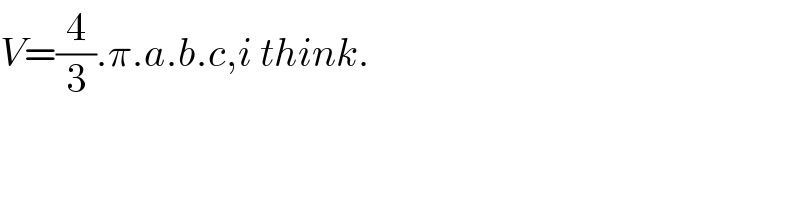
$${V}=\frac{\mathrm{4}}{\mathrm{3}}.\pi.{a}.{b}.{c},{i}\:{think}. \\ $$
Answered by ajfour last updated on 15/May/18

$${At}\:{a}\:{chosen}\:{z}=\:{constant}\:<\:{c} \\ $$$${the}\:\:{eq}.\:{of}\:{cross}\:{section}\:{of} \\ $$$${ellipsoid}\:\bot\:{to}\:{z}\:{axis}\:{is} \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} \left(\mathrm{1}−\frac{{z}^{\mathrm{2}} }{{c}^{\mathrm{2}} }\right)}+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} \left(\mathrm{1}−\frac{{z}^{\mathrm{2}} }{{c}^{\mathrm{2}} }\right)}\:=\mathrm{1} \\ $$$${cross}\:{sectional}\:{area} \\ $$$$\:\:\:\:\:=\:\pi{ab}\left(\mathrm{1}−\frac{{z}^{\mathrm{2}} }{{c}^{\mathrm{2}} }\right)\:. \\ $$$${V}=\int_{−{c}} ^{\:\:{c}} \pi{ab}\left(\mathrm{1}−\frac{{z}^{\mathrm{2}} }{{c}^{\mathrm{2}} }\right){dz} \\ $$$$ \\ $$$$\:\:\:\:=\mathrm{2}\pi{ab}\left({c}−\frac{{c}}{\mathrm{3}}\right)\:=\frac{\mathrm{4}\pi}{\mathrm{3}}{abc}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/May/18
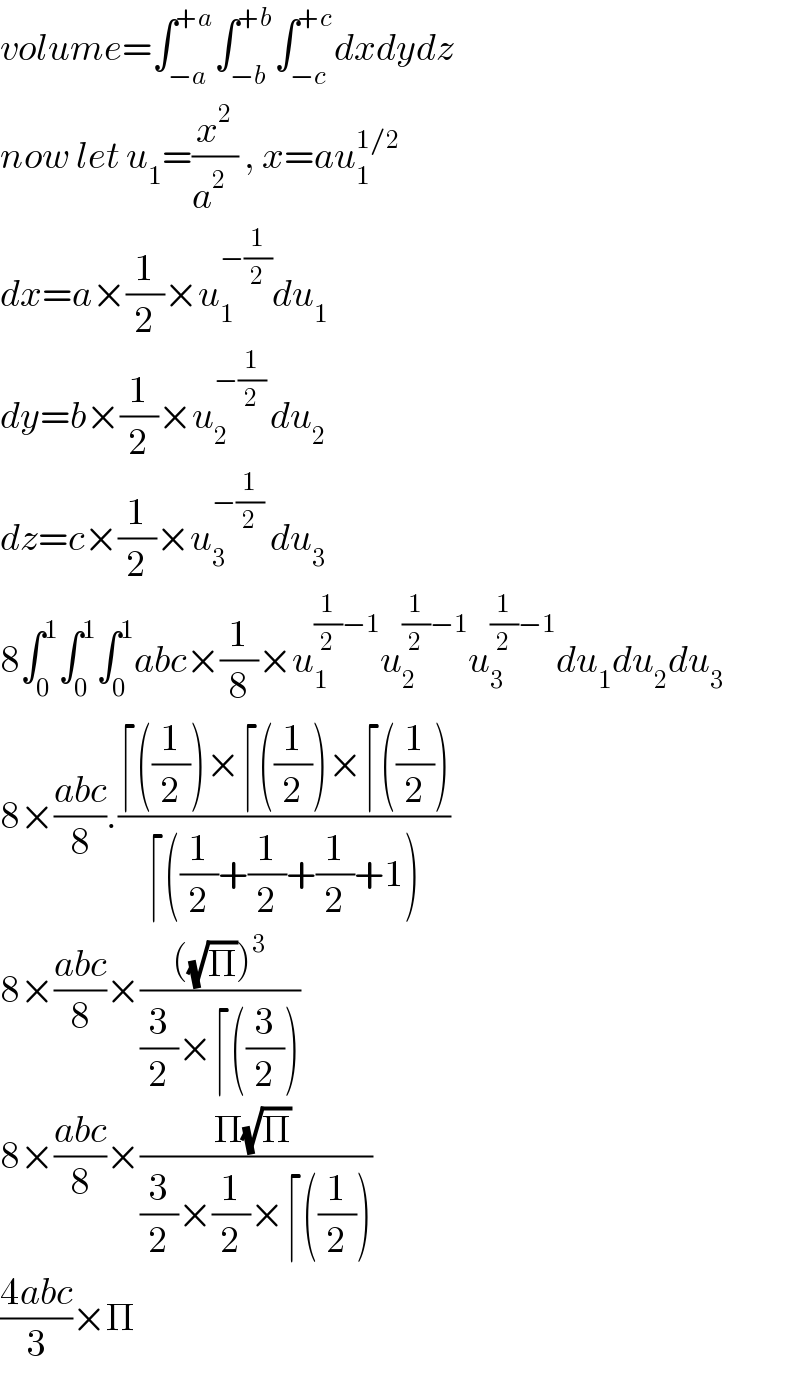
$${volume}=\int_{−{a}} ^{+{a}} \int_{−{b}} ^{+{b}} \int_{−{c}} ^{+{c}} {dxdydz} \\ $$$${now}\:{let}\:{u}_{\mathrm{1}} =\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} \:\:}\:,\:{x}={au}_{\mathrm{1}} ^{\mathrm{1}/\mathrm{2}} \\ $$$${dx}={a}×\frac{\mathrm{1}}{\mathrm{2}}×{u}_{\mathrm{1}} ^{−\frac{\mathrm{1}}{\mathrm{2}}} {du}_{\mathrm{1}} \\ $$$${dy}={b}×\frac{\mathrm{1}}{\mathrm{2}}×{u}_{\mathrm{2}} ^{−\frac{\mathrm{1}}{\mathrm{2}}\:} {du}_{\mathrm{2}} \\ $$$${dz}={c}×\frac{\mathrm{1}}{\mathrm{2}}×{u}_{\mathrm{3}} ^{−\frac{\mathrm{1}}{\mathrm{2}}} \:{du}_{\mathrm{3}} \\ $$$$\mathrm{8}\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} {abc}×\frac{\mathrm{1}}{\mathrm{8}}×{u}_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {u}_{\mathrm{2}} ^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {u}_{\mathrm{3}} ^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {du}_{\mathrm{1}} {du}_{\mathrm{2}} {du}_{\mathrm{3}} \\ $$$$\mathrm{8}×\frac{{abc}}{\mathrm{8}}.\frac{\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}\right)×\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}\right)×\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right)} \\ $$$$\mathrm{8}×\frac{{abc}}{\mathrm{8}}×\frac{\left(\sqrt{\Pi}\right)^{\mathrm{3}} }{\frac{\mathrm{3}}{\mathrm{2}}×\lceil\left(\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$$$\mathrm{8}×\frac{{abc}}{\mathrm{8}}×\frac{\Pi\sqrt{\Pi}\:}{\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}×\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$\frac{\mathrm{4}{abc}}{\mathrm{3}}×\Pi \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 15/May/18

Commented by tanmay.chaudhury50@gmail.com last updated on 15/May/18
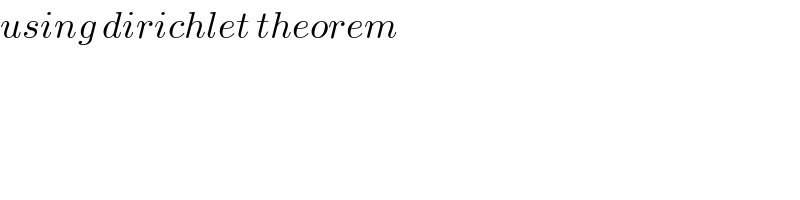
$${using}\:{dirichlet}\:{theorem} \\ $$
Commented by ajfour last updated on 15/May/18

$${thanks}. \\ $$
