Question-100817

Question Number 100817 by ajfour last updated on 28/Jun/20

Commented by ajfour last updated on 28/Jun/20

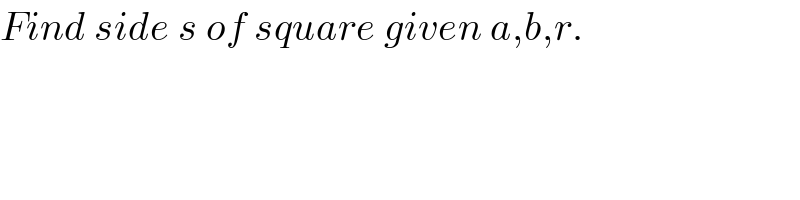
$${Find}\:{side}\:{s}\:{of}\:{square}\:{given}\:{a},{b},{r}. \\ $$

Answered by mr W last updated on 28/Jun/20

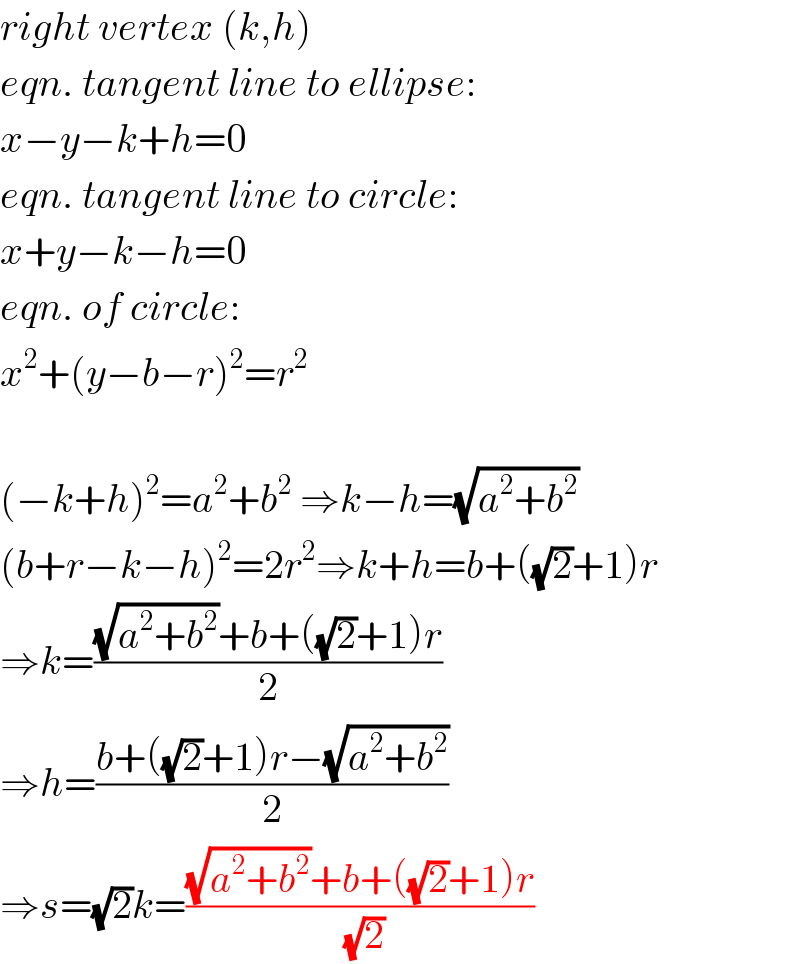
right vertex (k,h) eqn. tangent line to ellipse: x−y−k+h=0 eqn. tangent line to circle: x+y−k−h=0 eqn. of circle: x^2 +(y−b−r)^2 =r^2 (−k+h)^2 =a^2 +b^2 ⇒k−h=(√(a^2 +b^2 )) (b+r−k−h)^2 =2r^2 ⇒k+h=b+((√2)+1)r ⇒k=(((√(a^2 +b^2 ))+b+((√2)+1)r)/2) ⇒h=((b+((√2)+1)r−(√(a^2 +b^2 )))/2) ⇒s=(√2)k=(((√(a^2 +b^2 ))+b+((√2)+1)r)/( (√2)))

$${right}\:{vertex}\:\left({k},{h}\right) \\ $$$${eqn}.\:{tangent}\:{line}\:{to}\:{ellipse}: \\ $$$${x}−{y}−{k}+{h}=\mathrm{0} \\ $$$${eqn}.\:{tangent}\:{line}\:{to}\:{circle}: \\ $$$${x}+{y}−{k}−{h}=\mathrm{0} \\ $$$${eqn}.\:{of}\:{circle}: \\ $$$${x}^{\mathrm{2}} +\left({y}−{b}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$ \\ $$$$\left(−{k}+{h}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \:\Rightarrow{k}−{h}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\left({b}+{r}−{k}−{h}\right)^{\mathrm{2}} =\mathrm{2}{r}^{\mathrm{2}} \Rightarrow{k}+{h}={b}+\left(\sqrt{\mathrm{2}}+\mathrm{1}\right){r} \\ $$$$\Rightarrow{k}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+{b}+\left(\sqrt{\mathrm{2}}+\mathrm{1}\right){r}}{\mathrm{2}} \\ $$$$\Rightarrow{h}=\frac{{b}+\left(\sqrt{\mathrm{2}}+\mathrm{1}\right){r}−\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\Rightarrow{s}=\sqrt{\mathrm{2}}{k}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+{b}+\left(\sqrt{\mathrm{2}}+\mathrm{1}\right){r}}{\:\sqrt{\mathrm{2}}} \\ $$

Commented by mr W last updated on 28/Jun/20

Commented by ajfour last updated on 28/Jun/20

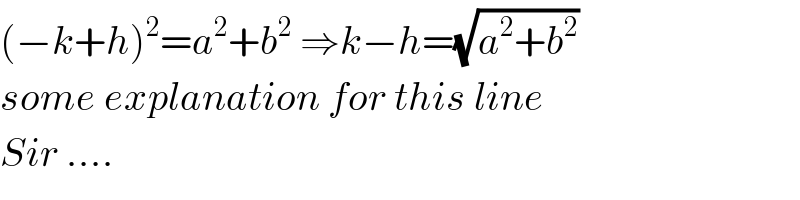
(−k+h)^2 =a^2 +b^2 ⇒k−h=(√(a^2 +b^2 )) some explanation for this line Sir ....

$$\left(−{k}+{h}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \:\Rightarrow{k}−{h}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${some}\:{explanation}\:{for}\:{this}\:{line} \\ $$$${Sir}\:…. \\ $$

Commented by mr W last updated on 28/Jun/20

if y=mx+c tangents the ellipse, then a^2 m^2 +b^2 =c^2 . i think once you have proved this.

$${if}\:{y}={mx}+{c}\:{tangents}\:{the}\:{ellipse},\:{then} \\ $$$${a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} ={c}^{\mathrm{2}} . \\ $$$${i}\:{think}\:{once}\:{you}\:{have}\:{proved}\:{this}. \\ $$

Commented by ajfour last updated on 29/Jun/20

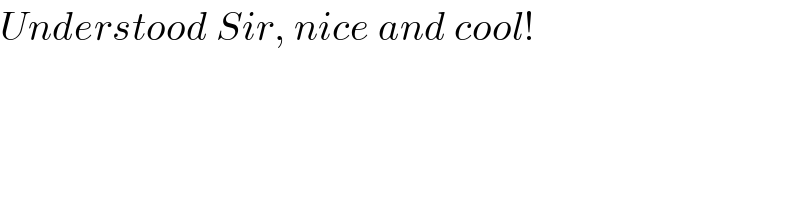
$${Understood}\:{Sir},\:{nice}\:{and}\:{cool}! \\ $$

Answered by ajfour last updated on 29/Jun/20

{(b+r+r(√2))−s(√2) }^2 =a^2 +b^2 ⇒ s=(((√(a^2 +b^2 ))+b+r(1+(√2)))/( (√2))) .

$$\left\{\left({b}+{r}+{r}\sqrt{\mathrm{2}}\right)−{s}\sqrt{\mathrm{2}}\:\right\}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{s}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+{b}+{r}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}}\:. \\ $$

Commented by ajfour last updated on 29/Jun/20

$${your}\:{idea}\:{implemented}\:{straightway}, \\ $$$${Sir}. \\ $$

Commented by mr W last updated on 29/Jun/20

��

Facebook Tweet Pin

Leave a Reply Cancel reply