Question Number 35319 by Tinkutara last updated on 17/May/18

Answered by MJS last updated on 17/May/18
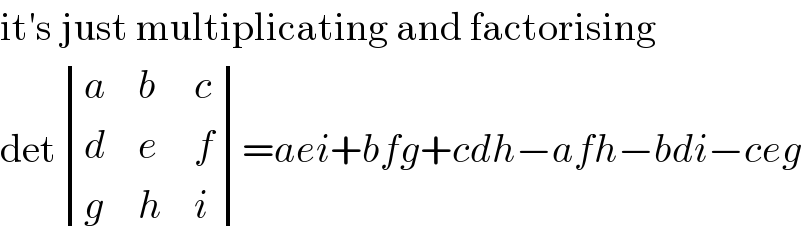
$$\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{multiplicating}\:\mathrm{and}\:\mathrm{factorising} \\ $$$$\mathrm{det}\begin{vmatrix}{{a}}&{{b}}&{{c}}\\{{d}}&{{e}}&{{f}}\\{{g}}&{{h}}&{{i}}\end{vmatrix}={aei}+{bfg}+{cdh}−{afh}−{bdi}−{ceg} \\ $$
Commented by Tinkutara last updated on 18/May/18
No it is to be done by properties of determinants. Please can you try that way?
Answered by ajfour last updated on 18/May/18
![determinant ((((b+c)^2 ),a^2 ,a^2 ),(b^2 ,((c+a)^2 ),b^2 ),(c^2 ,c^2 ,((a+b)^2 ))) C_1 →C_1 −C_3 ; C_2 →C_2 −C_3 = determinant ((((b+c+a)(b+c−a)),0,a^2 ),(0,((c+a+b)(c+a−b)),b^2 ),(((c+a+b)(c−a−b)),((c+a+b)(c−a−b)),((a+b)^2 ))) =(a+b+c)^2 determinant (((b+c−a),0,a^2 ),(0,(c+a−b),b^2 ),((c−a−b),(c−a−b),((a+b)^2 ))) R_3 →R_3 −(R_1 +R_2 ) =(a+b+c)^2 determinant (((b+c−a),0,a^2 ),(0,(c+a−b),b^2 ),((−2b),(−2a),(2ab))) =(a+b+c)^2 {(b+c−a)[2abc+2a^2 b] +a^2 [2bc+2ab−2b^2 ]} =(a+b+c)^2 {2b[abc+ac^2 −a^2 c a^2 b+a^2 c−a^3 +a^2 c+a^3 −a^2 b]} =(a+b+c)^2 {2b[abc+ac^2 +a^2 c} =2abc(a+b+c)^2 (b+c+a) =2abc(a+b+c)^3 .](https://www.tinkutara.com/question/Q35376.png)
$$\begin{vmatrix}{\left({b}+{c}\right)^{\mathrm{2}} }&{{a}^{\mathrm{2}} }&{{a}^{\mathrm{2}} }\\{{b}^{\mathrm{2}} }&{\left({c}+{a}\right)^{\mathrm{2}} }&{{b}^{\mathrm{2}} }\\{{c}^{\mathrm{2}} }&{{c}^{\mathrm{2}} }&{\left({a}+{b}\right)^{\mathrm{2}} }\end{vmatrix} \\ $$$${C}_{\mathrm{1}} \rightarrow{C}_{\mathrm{1}} −{C}_{\mathrm{3}} ;\:\:{C}_{\mathrm{2}} \rightarrow{C}_{\mathrm{2}} −{C}_{\mathrm{3}} \: \\ $$$$=\begin{vmatrix}{\left({b}+{c}+{a}\right)\left({b}+{c}−{a}\right)}&{\mathrm{0}}&{{a}^{\mathrm{2}} }\\{\mathrm{0}}&{\left({c}+{a}+{b}\right)\left({c}+{a}−{b}\right)}&{{b}^{\mathrm{2}} }\\{\left({c}+{a}+{b}\right)\left({c}−{a}−{b}\right)}&{\left({c}+{a}+{b}\right)\left({c}−{a}−{b}\right)}&{\left({a}+{b}\right)^{\mathrm{2}} }\end{vmatrix} \\ $$$$ \\ $$$$=\left({a}+{b}+{c}\right)^{\mathrm{2}} \begin{vmatrix}{{b}+{c}−{a}}&{\mathrm{0}}&{{a}^{\mathrm{2}} }\\{\mathrm{0}}&{{c}+{a}−{b}}&{{b}^{\mathrm{2}} }\\{{c}−{a}−{b}}&{{c}−{a}−{b}}&{\left({a}+{b}\right)^{\mathrm{2}} }\end{vmatrix} \\ $$$${R}_{\mathrm{3}} \rightarrow{R}_{\mathrm{3}} −\left({R}_{\mathrm{1}} +{R}_{\mathrm{2}} \right) \\ $$$$=\left({a}+{b}+{c}\right)^{\mathrm{2}} \begin{vmatrix}{{b}+{c}−{a}}&{\mathrm{0}}&{{a}^{\mathrm{2}} }\\{\mathrm{0}}&{{c}+{a}−{b}}&{{b}^{\mathrm{2}} }\\{−\mathrm{2}{b}}&{−\mathrm{2}{a}}&{\mathrm{2}{ab}}\end{vmatrix} \\ $$$$=\left({a}+{b}+{c}\right)^{\mathrm{2}} \left\{\left({b}+{c}−{a}\right)\left[\mathrm{2}{abc}+\mathrm{2}{a}^{\mathrm{2}} {b}\right]\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{a}^{\mathrm{2}} \left[\mathrm{2}{bc}+\mathrm{2}{ab}−\mathrm{2}{b}^{\mathrm{2}} \right]\right\} \\ $$$$=\left({a}+{b}+{c}\right)^{\mathrm{2}} \left\{\mathrm{2}{b}\left[{abc}+{ac}^{\mathrm{2}} −{a}^{\mathrm{2}} {c}\right.\right. \\ $$$$\left.\:\left.\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{2}} {b}+{a}^{\mathrm{2}} {c}−{a}^{\mathrm{3}} +{a}^{\mathrm{2}} {c}+{a}^{\mathrm{3}} −{a}^{\mathrm{2}} {b}\right]\right\} \\ $$$$=\left({a}+{b}+{c}\right)^{\mathrm{2}} \left\{\mathrm{2}{b}\left[{abc}+{ac}^{\mathrm{2}} +{a}^{\mathrm{2}} {c}\right\}\right. \\ $$$$=\mathrm{2}{abc}\left({a}+{b}+{c}\right)^{\mathrm{2}} \left({b}+{c}+{a}\right) \\ $$$$=\mathrm{2}{abc}\left({a}+{b}+{c}\right)^{\mathrm{3}} \:. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 18/May/18

$${pls}\:{let}\:{me}\:{know}\:{how}\:{to}\:{put}\:{determinant}\:{sign} \\ $$$${in}\:{this}\:{app} \\ $$
Commented by ajfour last updated on 18/May/18
$${i}\:{couldn}'{t}\:{find}\:{a}\:{way}\:{like}\:{that}.. \\ $$
Commented by Tinkutara last updated on 18/May/18

$${Should}\:{not}\:{we}\:{simplify}\:{the}\:{determinant} \\ $$$${till}\:{atleast}\:\mathrm{2}\:{zeroes}\:{in}\:{any}\:{row}\:{or} \\ $$$${column}? \\ $$
