Question Number 35384 by 7991 last updated on 18/May/18
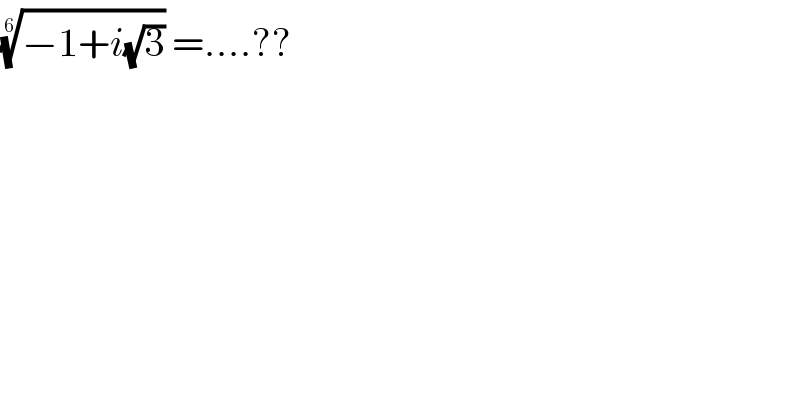
$$\sqrt[{\mathrm{6}}]{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}\:=….?? \\ $$
Commented by prof Abdo imad last updated on 18/May/18
![the 6^(eme) roots of −1+i(√3) are the complex z_k wich verify z_k ^6 = −1+i(√3) let solve z^6 =−1+i(√3) z=r e^(iθ) ∣−1+i(√3)∣=2 ⇒−1+i(√3) =2(−(1/2) +i((√3)/2)) =2e^(i((2π)/3)) so z^6 =−1+i(√3) ⇔r^6 e^(i(6θ)) = 2 e^(i((2π)/3)) ⇒ r = 2^(1/6) and 6θ= ((2π)/3) +2kπ ⇒r=^6 (√2) θ= (π/9) +((kπ)/3) k∈[[0,5]]⇒ z_k =^6 (√2) e^(i((π/9) +((kπ)/3))) with k∈[0,5] .](https://www.tinkutara.com/question/Q35393.png)
$${the}\:\mathrm{6}^{{eme}} \:{roots}\:{of}\:−\mathrm{1}+{i}\sqrt{\mathrm{3}}\:\:{are}\:{the}\:{complex}\:{z}_{{k}} \\ $$$${wich}\:{verify}\:{z}_{{k}} ^{\mathrm{6}} =\:−\mathrm{1}+{i}\sqrt{\mathrm{3}}\:\:\:{let}\:{solve}\:{z}^{\mathrm{6}} =−\mathrm{1}+{i}\sqrt{\mathrm{3}} \\ $$$${z}={r}\:{e}^{{i}\theta} \:\:\:\:\:\:\mid−\mathrm{1}+{i}\sqrt{\mathrm{3}}\mid=\mathrm{2}\:\Rightarrow−\mathrm{1}+{i}\sqrt{\mathrm{3}}\:=\mathrm{2}\left(−\frac{\mathrm{1}}{\mathrm{2}}\:+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:\:\:{so}\:\:{z}^{\mathrm{6}} =−\mathrm{1}+{i}\sqrt{\mathrm{3}}\:\Leftrightarrow{r}^{\mathrm{6}} \:{e}^{{i}\left(\mathrm{6}\theta\right)} =\:\mathrm{2}\:{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:\Rightarrow \\ $$$${r}\:=\:\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{6}}} \:\:\:{and}\:\mathrm{6}\theta=\:\frac{\mathrm{2}\pi}{\mathrm{3}}\:+\mathrm{2}{k}\pi\:\Rightarrow{r}=^{\mathrm{6}} \sqrt{\mathrm{2}} \\ $$$$\theta=\:\frac{\pi}{\mathrm{9}}\:+\frac{{k}\pi}{\mathrm{3}}\:\:\:\:{k}\in\left[\left[\mathrm{0},\mathrm{5}\right]\right]\Rightarrow\:{z}_{{k}} =^{\mathrm{6}} \sqrt{\mathrm{2}}\:\:{e}^{{i}\left(\frac{\pi}{\mathrm{9}}\:+\frac{{k}\pi}{\mathrm{3}}\right)} \:{with} \\ $$$${k}\in\left[\mathrm{0},\mathrm{5}\right]\:. \\ $$
Answered by MJS last updated on 18/May/18
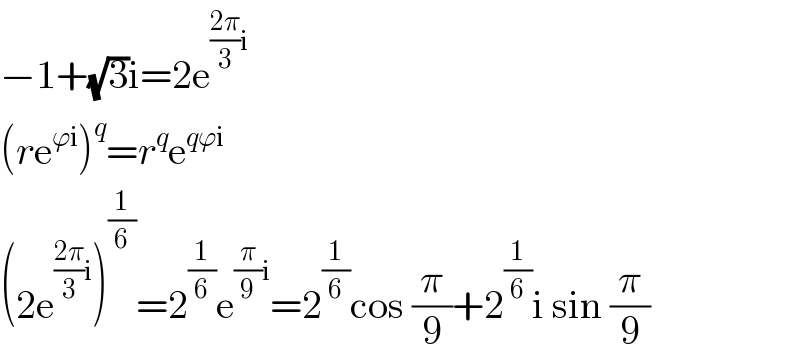
$$−\mathrm{1}+\sqrt{\mathrm{3}}\mathrm{i}=\mathrm{2e}^{\frac{\mathrm{2}\pi}{\mathrm{3}}\mathrm{i}} \\ $$$$\left({r}\mathrm{e}^{\varphi\mathrm{i}} \right)^{{q}} ={r}^{{q}} \mathrm{e}^{{q}\varphi\mathrm{i}} \\ $$$$\left(\mathrm{2e}^{\frac{\mathrm{2}\pi}{\mathrm{3}}\mathrm{i}} \right)^{\frac{\mathrm{1}}{\mathrm{6}}} =\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{6}}} \mathrm{e}^{\frac{\pi}{\mathrm{9}}\mathrm{i}} =\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{6}}} \mathrm{cos}\:\frac{\pi}{\mathrm{9}}+\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{6}}} \mathrm{i}\:\mathrm{sin}\:\frac{\pi}{\mathrm{9}} \\ $$
