Menu Close

let-m-gt-0-and-0-lt-a-lt-b-1-calculate-0-cos-mx-x-2-a-2-x-2-b-2-dx-2-find-the-value-of-0-cos-2x-x-2-1-x-2-3-dx-

Tinku Tara 0 Comments
Pin




Question Number 35438 by prof Abdo imad last updated on 19/May/18
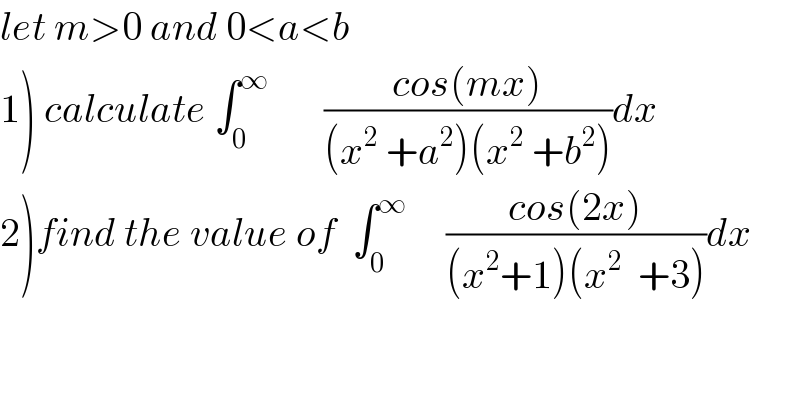
let m>0 and 0<a<b 1) calculate ∫_0 ^∞ ((cos(mx))/((x^2 +a^2 )(x^2 +b^2 )))dx 2)find the value of ∫_0 ^∞ ((cos(2x))/((x^2 +1)(x^2 +3)))dx
$${let}\:{m}>\mathrm{0}\:{and}\:\mathrm{0}<{a}<{b}\: \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\:\frac{{cos}\left({mx}\right)}{\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \right)}{dx} \\ $$$$\left.\mathrm{2}\right){find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{cos}\left(\mathrm{2}{x}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} \:\:+\mathrm{3}\right)}{dx} \\ $$
Commented by prof Abdo imad last updated on 21/May/18
let put I = ∫_0 ^∞ ((cos(mx))/((x^2 +a^2 )(x^(2 ) +b^2 )))dx 2I = ∫_(−∞) ^(+∞) ((cos(mx))/((x^2 +a^2 )(x^2 +b^2 )))dx =Re( ∫_(−∞) ^(+∞) (e^(imx) /((x^2 +a^2 )(x^2 +b^2 )))dx) let consider the complex function ϕ(z) = (e^(imz) /((x^2 +a^2 )(x^2 +b^2 ))) ϕ(z) = (e^(imz) /((x−ia)(x+ia)(x−ib)(x+ib))) thepoles of ϕ are ia,−ia,ib,−ib ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ { Res(ϕ,ia) +Res(ϕ,ib)} Res(ϕ,ia) = (e^(im(ia)) /(2ia(b^2 −a^2 ))) = (e^(−ma) /(2ia(b^2 −a^2 ))) Res(ϕ,ib) = (e^(im(ib)) /(2ib(a^2 −b^2 ))) = (e^(−mb) /(2ib(a^2 −b^2 ))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ (e^(−ma) /(2ia(b^2 −a^2 ))) + (e^(−mb) /(2ib(a^2 −b^2 )))} = (π/a) (e^(−ma) /(b^2 −a^2 )) −(π/b) (e^(−mb) /(b^2 −a^2 )) = (π/(b^2 −a^2 )){ (e^(−ma) /a) − (e^(−mb) /b)} ⇒ I = (π/(2(a^2 −b^2 ))){ (e^(−mb) /b) −(e^(−ma) /a)} 2)let take m=2 , a =1, b=(√3) we get ∫_0 ^∞ ((cos(2x))/((x^2 +1)(x^2 +3))) = (π/(2(1 −3))){ (e^(−2(√3)) /( (√3))) −(e^(−2) /1) } =−(π/4){ (e^(−2(√3)) /( (√3))) − e^(−2) } = (π/4){ e^(−2) − (e^(−2(√3)) /( (√3)))}.
$${let}\:{put}\:{I}\:\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\:\frac{{cos}\left({mx}\right)}{\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}\:} \:+{b}^{\mathrm{2}} \right)}{dx} \\ $$$$\mathrm{2}{I}\:=\:\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{cos}\left({mx}\right)}{\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \right)}{dx} \\ $$$$={Re}\left(\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\:\frac{{e}^{{imx}} }{\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \right)}{dx}\right)\:{let}\:{consider} \\ $$$${the}\:{complex}\:{function} \\ $$$$\varphi\left({z}\right)\:=\:\frac{{e}^{{imz}} }{\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \right)} \\ $$$$\varphi\left({z}\right)\:=\:\frac{{e}^{{imz}} }{\left({x}−{ia}\right)\left({x}+{ia}\right)\left({x}−{ib}\right)\left({x}+{ib}\right)}\:\:{thepoles} \\ $$$${of}\:\varphi\:{are}\:\:{ia},−{ia},{ib},−{ib} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\left\{\:{Res}\left(\varphi,{ia}\right)\:+{Res}\left(\varphi,{ib}\right)\right\} \\ $$$${Res}\left(\varphi,{ia}\right)\:=\:\frac{{e}^{{im}\left({ia}\right)} }{\mathrm{2}{ia}\left({b}^{\mathrm{2}} \:−{a}^{\mathrm{2}} \right)}\:=\:\frac{{e}^{−{ma}} }{\mathrm{2}{ia}\left({b}^{\mathrm{2}} \:−{a}^{\mathrm{2}} \right)} \\ $$$${Res}\left(\varphi,{ib}\right)\:=\:\:\frac{{e}^{{im}\left({ib}\right)} }{\mathrm{2}{ib}\left({a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} \right)}\:=\:\frac{{e}^{−{mb}} }{\mathrm{2}{ib}\left({a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} \right)} \\ $$$$\int_{−\infty} ^{+\infty} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:\:\frac{{e}^{−{ma}} }{\mathrm{2}{ia}\left({b}^{\mathrm{2}} \:−{a}^{\mathrm{2}} \right)}\:+\:\:\frac{{e}^{−{mb}} }{\mathrm{2}{ib}\left({a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} \right)}\right\} \\ $$$$=\:\frac{\pi}{{a}}\:\frac{{e}^{−{ma}} }{{b}^{\mathrm{2}} \:−{a}^{\mathrm{2}} }\:−\frac{\pi}{{b}}\:\:\frac{{e}^{−{mb}} }{{b}^{\mathrm{2}} \:−{a}^{\mathrm{2}} } \\ $$$$=\:\frac{\pi}{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }\left\{\:\:\frac{{e}^{−{ma}} }{{a}}\:−\:\frac{{e}^{−{mb}} }{{b}}\right\}\:\Rightarrow \\ $$$${I}\:=\:\frac{\pi}{\mathrm{2}\left({a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} \right)}\left\{\:\:\frac{{e}^{−{mb}} }{{b}}\:\:−\frac{{e}^{−{ma}} }{{a}}\right\} \\ $$$$\left.\mathrm{2}\right){let}\:{take}\:{m}=\mathrm{2}\:,\:{a}\:=\mathrm{1},\:{b}=\sqrt{\mathrm{3}}\:\:{we}\:{get} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{cos}\left(\mathrm{2}{x}\right)}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)}\:=\:\frac{\pi}{\mathrm{2}\left(\mathrm{1}\:−\mathrm{3}\right)}\left\{\:\frac{{e}^{−\mathrm{2}\sqrt{\mathrm{3}}} }{\:\sqrt{\mathrm{3}}}\:−\frac{{e}^{−\mathrm{2}} }{\mathrm{1}}\:\right\} \\ $$$$=−\frac{\pi}{\mathrm{4}}\left\{\:\:\frac{{e}^{−\mathrm{2}\sqrt{\mathrm{3}}} }{\:\sqrt{\mathrm{3}}}\:−\:{e}^{−\mathrm{2}} \right\}\:=\:\frac{\pi}{\mathrm{4}}\left\{\:{e}^{−\mathrm{2}} \:\:−\:\frac{{e}^{−\mathrm{2}\sqrt{\mathrm{3}}} }{\:\sqrt{\mathrm{3}}}\right\}. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *