Question Number 68961 by ahmadshah last updated on 17/Sep/19
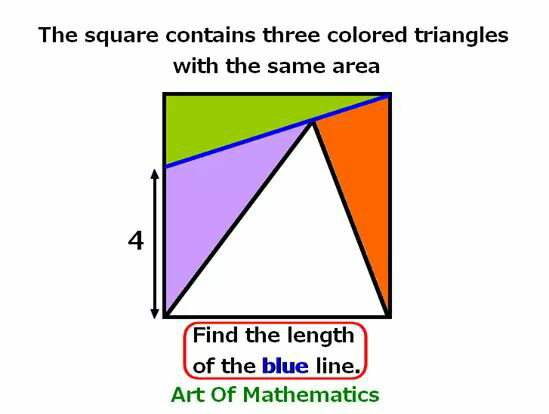
Answered by mr W last updated on 17/Sep/19
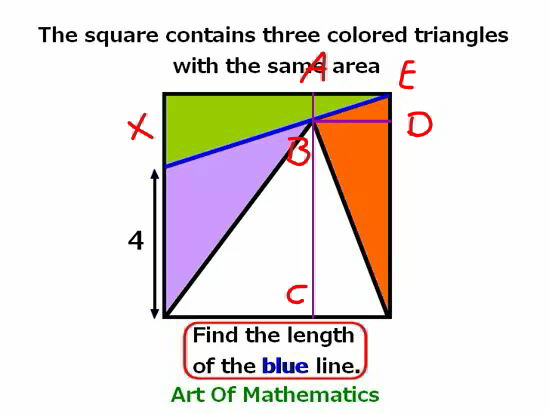
Commented by mr W last updated on 17/Sep/19
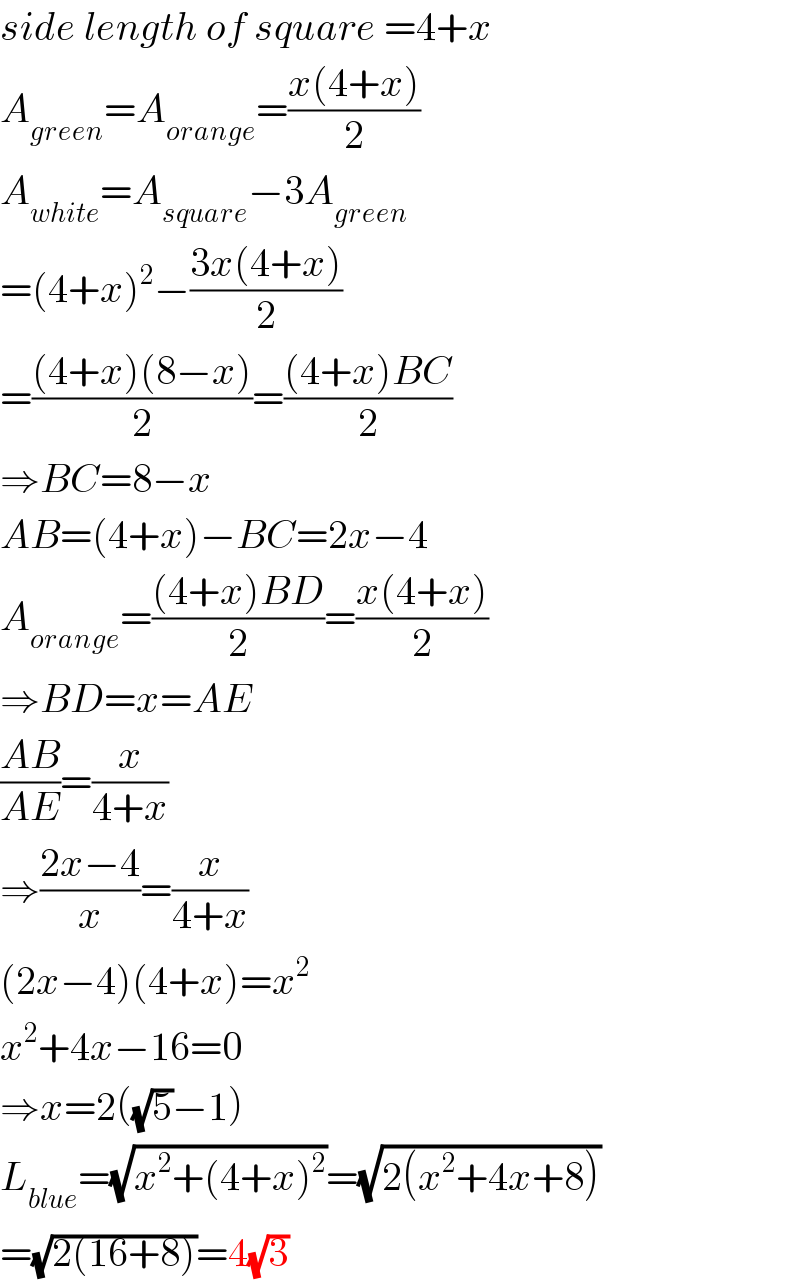
$${side}\:{length}\:{of}\:{square}\:=\mathrm{4}+{x} \\ $$$${A}_{{green}} ={A}_{{orange}} =\frac{{x}\left(\mathrm{4}+{x}\right)}{\mathrm{2}} \\ $$$${A}_{{white}} ={A}_{{square}} −\mathrm{3}{A}_{{green}} \\ $$$$=\left(\mathrm{4}+{x}\right)^{\mathrm{2}} −\frac{\mathrm{3}{x}\left(\mathrm{4}+{x}\right)}{\mathrm{2}} \\ $$$$=\frac{\left(\mathrm{4}+{x}\right)\left(\mathrm{8}−{x}\right)}{\mathrm{2}}=\frac{\left(\mathrm{4}+{x}\right){BC}}{\mathrm{2}} \\ $$$$\Rightarrow{BC}=\mathrm{8}−{x} \\ $$$${AB}=\left(\mathrm{4}+{x}\right)−{BC}=\mathrm{2}{x}−\mathrm{4} \\ $$$${A}_{{orange}} =\frac{\left(\mathrm{4}+{x}\right){BD}}{\mathrm{2}}=\frac{{x}\left(\mathrm{4}+{x}\right)}{\mathrm{2}} \\ $$$$\Rightarrow{BD}={x}={AE} \\ $$$$\frac{{AB}}{{AE}}=\frac{{x}}{\mathrm{4}+{x}} \\ $$$$\Rightarrow\frac{\mathrm{2}{x}−\mathrm{4}}{{x}}=\frac{{x}}{\mathrm{4}+{x}} \\ $$$$\left(\mathrm{2}{x}−\mathrm{4}\right)\left(\mathrm{4}+{x}\right)={x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{16}=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{2}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right) \\ $$$${L}_{{blue}} =\sqrt{{x}^{\mathrm{2}} +\left(\mathrm{4}+{x}\right)^{\mathrm{2}} }=\sqrt{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{8}\right)} \\ $$$$=\sqrt{\mathrm{2}\left(\mathrm{16}+\mathrm{8}\right)}=\mathrm{4}\sqrt{\mathrm{3}} \\ $$
