Question Number 166584 by amin96 last updated on 22/Feb/22

Commented by bobhans last updated on 22/Feb/22
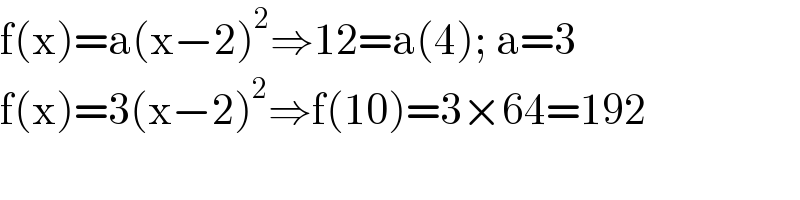
$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{a}\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} \Rightarrow\mathrm{12}=\mathrm{a}\left(\mathrm{4}\right);\:\mathrm{a}=\mathrm{3} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{3}\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} \Rightarrow\mathrm{f}\left(\mathrm{10}\right)=\mathrm{3}×\mathrm{64}=\mathrm{192} \\ $$
Answered by nurtani last updated on 22/Feb/22
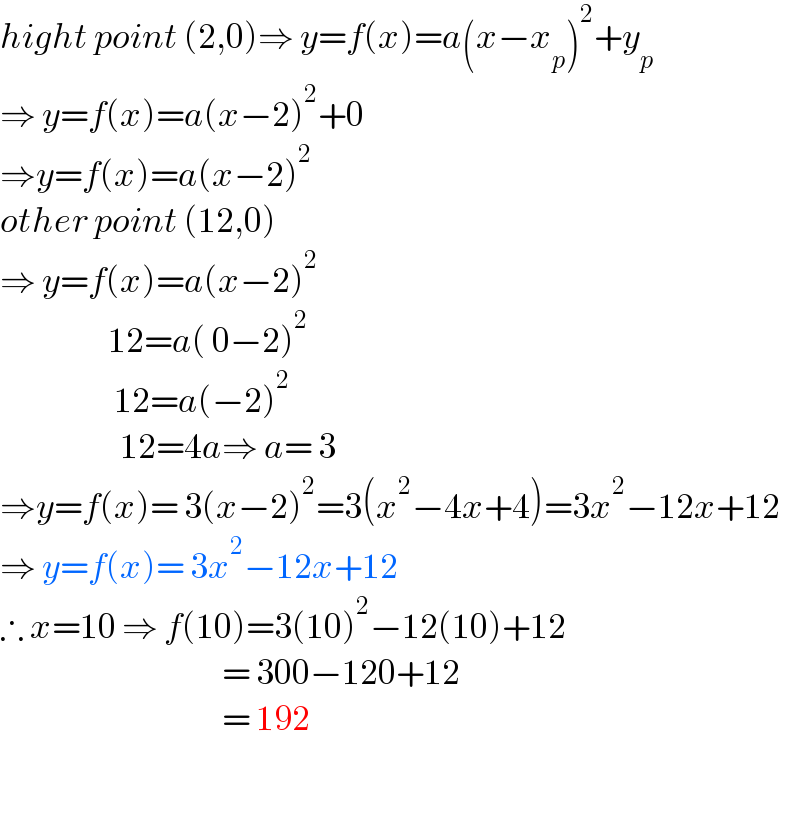
$${hight}\:{point}\:\left(\mathrm{2},\mathrm{0}\right)\Rightarrow\:{y}={f}\left({x}\right)={a}\left({x}−{x}_{{p}} \right)^{\mathrm{2}} +{y}_{{p}} \\ $$$$\Rightarrow\:{y}={f}\left({x}\right)={a}\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{0} \\ $$$$\Rightarrow{y}={f}\left({x}\right)={a}\left({x}−\mathrm{2}\right)^{\mathrm{2}} \\ $$$${other}\:{point}\:\left(\mathrm{12},\mathrm{0}\right) \\ $$$$\Rightarrow\:{y}={f}\left({x}\right)={a}\left({x}−\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{12}={a}\left(\:\mathrm{0}−\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{12}={a}\left(−\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{12}=\mathrm{4}{a}\Rightarrow\:{a}=\:\mathrm{3} \\ $$$$\Rightarrow{y}={f}\left({x}\right)=\:\mathrm{3}\left({x}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{3}\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}\right)=\mathrm{3}{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{12} \\ $$$$\Rightarrow\:{y}={f}\left({x}\right)=\:\mathrm{3}{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{12}\: \\ $$$$\therefore\:{x}=\mathrm{10}\:\Rightarrow\:{f}\left(\mathrm{10}\right)=\mathrm{3}\left(\mathrm{10}\right)^{\mathrm{2}} −\mathrm{12}\left(\mathrm{10}\right)+\mathrm{12} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{300}−\mathrm{120}+\mathrm{12} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{192}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
