Menu Close

Question-134526

Tinku Tara 0 Comments
Pin




Question Number 134526 by mohammad17 last updated on 04/Mar/21
Answered by mr W last updated on 05/Mar/21
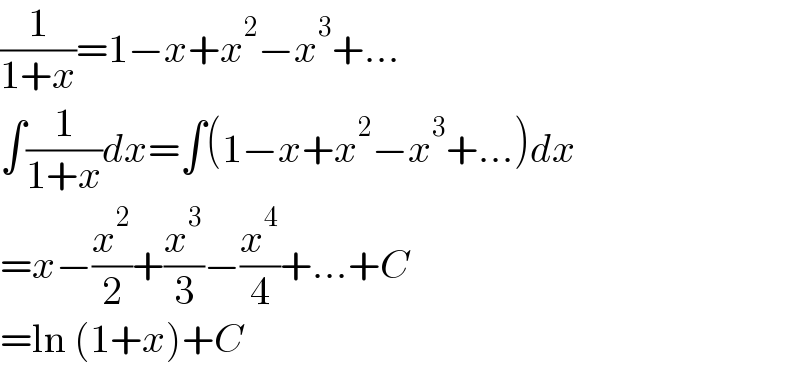
(1/(1+x))=1−x+x^2 −x^3 +... ∫(1/(1+x))dx=∫(1−x+x^2 −x^3 +...)dx =x−(x^2 /2)+(x^3 /3)−(x^4 /4)+...+C =ln (1+x)+C
$$\frac{\mathrm{1}}{\mathrm{1}+{x}}=\mathrm{1}−{x}+{x}^{\mathrm{2}} −{x}^{\mathrm{3}} +… \\ $$$$\int\frac{\mathrm{1}}{\mathrm{1}+{x}}{dx}=\int\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} −{x}^{\mathrm{3}} +…\right){dx} \\ $$$$={x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{{x}^{\mathrm{4}} }{\mathrm{4}}+…+{C} \\ $$$$=\mathrm{ln}\:\left(\mathrm{1}+{x}\right)+{C} \\ $$
Commented by mathmax by abdo last updated on 05/Mar/21
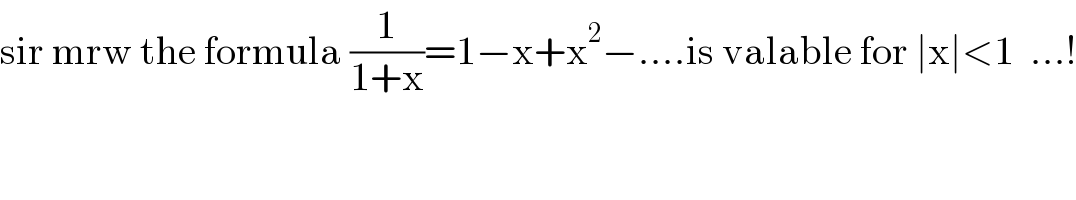
sir mrw the formula (1/(1+x))=1−x+x^2 −....is valable for ∣x∣<1 ...!
$$\mathrm{sir}\:\mathrm{mrw}\:\mathrm{the}\:\mathrm{formula}\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}=\mathrm{1}−\mathrm{x}+\mathrm{x}^{\mathrm{2}} −….\mathrm{is}\:\mathrm{valable}\:\mathrm{for}\:\mid\mathrm{x}\mid<\mathrm{1}\:\:…! \\ $$
Commented by mr W last updated on 05/Mar/21
yes, i know. basically you are absolutely right. but both for ∣x∣<1 and for ∣x∣>1 we get the same. so we can here treat x just as a symbol despite its concrete values. here the proof for ∣x∣>1: ∣x∣>1 ⇒∣(1/x)∣<1 (1/(1+x))=((1/x)/(1+(1/x)))=1−(1/(1+(1/x)))=1−(1−(1/x)+(1/x^2 )−(1/x^3 )+...) (1/(1+x))=(1/x)−(1/x^2 )+(1/x^3 )−(1/x^4 )+... ∫(1/(1+x))dx=ln x+((1/x)−(1/(2x^2 ))+(1/(3x^3 ))+...)+C ∫(1/(1+x))dx=ln x+ln (1+(1/x))+C ∫(1/(1+x))dx=ln (1+x)+C (∣x∣>1)
$${yes},\:{i}\:{know}.\:{basically}\:{you}\:{are} \\ $$$${absolutely}\:{right}.\:{but}\:{both}\:{for}\:\mid{x}\mid<\mathrm{1} \\ $$$${and}\:{for}\:\mid{x}\mid>\mathrm{1}\:{we}\:{get}\:{the}\:{same}.\:{so}\:{we} \\ $$$${can}\:{here}\:{treat}\:{x}\:{just}\:{as}\:{a}\:{symbol}\:\: \\ $$$${despite}\:{its}\:{concrete}\:{values}. \\ $$$${here}\:{the}\:{proof}\:{for}\:\mid{x}\mid>\mathrm{1}: \\ $$$$\mid{x}\mid>\mathrm{1}\:\Rightarrow\mid\frac{\mathrm{1}}{{x}}\mid<\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{x}}=\frac{\frac{\mathrm{1}}{{x}}}{\mathrm{1}+\frac{\mathrm{1}}{{x}}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{x}}}=\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}^{\mathrm{3}} }+…\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{x}}=\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{x}^{\mathrm{3}} }−\frac{\mathrm{1}}{{x}^{\mathrm{4}} }+… \\ $$$$\int\frac{\mathrm{1}}{\mathrm{1}+{x}}{dx}=\mathrm{ln}\:{x}+\left(\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{3}} }+…\right)+{C} \\ $$$$\int\frac{\mathrm{1}}{\mathrm{1}+{x}}{dx}=\mathrm{ln}\:{x}+\mathrm{ln}\:\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)+{C} \\ $$$$\int\frac{\mathrm{1}}{\mathrm{1}+{x}}{dx}=\mathrm{ln}\:\left(\mathrm{1}+{x}\right)+{C}\:\:\:\:\:\:\:\left(\mid{x}\mid>\mathrm{1}\right) \\ $$
Commented by mathmax by abdo last updated on 06/Mar/21
yes
$$\mathrm{yes} \\ $$
Answered by mathmax by abdo last updated on 05/Mar/21
let f(x)= ∫_x ^1 (dt/(1+t)) if o< x<1 ⇒o≤t≤1 ⇒ f(x)=∫_x ^1 Σ_(n=0) ^∞ (−1)^n t^n dt =Σ_(n=0) ^∞ (−1)^n ∫_x ^1 t^n dt =Σ_(n=0) ^∞ (((−1)^n )/(n+1))[t^(n+1) ]_x ^1 =Σ_(n=0) ^∞ (−1)^n ((1−x^(n+1) )/(n+1)) =−Σ_(n=1) ^∞ (−1)^(n−1) (x^n /n) +Σ_(n=0) ^∞ (((−1)^n )/(n+1)) =−ln(1+x)+ln(2) ⇒∫_1 ^x (dt/(1+t)) =ln(1+x)−ln(2) (c=−ln2) if x>1 we take g(x)=∫_1 ^x (dt/(1+t)) =_(t=(1/u)) ∫_1 ^(1/x) ((−du)/(u^2 (1+(1/u)))) =−∫_1 ^(1/x) (du/(u^2 +u)) =∫_(1/x) ^(1 ) (du/(u(u+1))) =∫_(1/x) ^1 (1/u)Σ_(n=0) ^∞ (−1)^n u^n du =Σ_(n=0) ^∞ (−1)^n ∫_(1/x) ^1 u^(n−1) du = =∫_(1/x) ^1 (du/u) +Σ_(n=1) ^∞ (−1)^n [(u^n /n)]_(1/x) ^1 =ln(x)+Σ_(n=1) ^∞ (((−1)^n )/n)(1−(1/x^n )) =ln(x)+Σ_(n=1) ^∞ (((−1)^n )/n)−Σ_(n=1) ^∞ (((−1)^n )/n)((1/x))^n =ln(x)−ln(2)+ln(1+(1/x)) =ln(1+x)−ln(2)
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\:\int_{\mathrm{x}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}}\:\:\:\:\:\mathrm{if}\:\mathrm{o}<\:\mathrm{x}<\mathrm{1}\:\Rightarrow\mathrm{o}\leqslant\mathrm{t}\leqslant\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\int_{\mathrm{x}} ^{\mathrm{1}} \sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{t}^{\mathrm{n}} \:\mathrm{dt}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{x}} ^{\mathrm{1}} \:\mathrm{t}^{\mathrm{n}} \:\mathrm{dt}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\left[\mathrm{t}^{\mathrm{n}+\mathrm{1}} \right]_{\mathrm{x}} ^{\mathrm{1}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\frac{\mathrm{1}−\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\:=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\:+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}} \\ $$$$=−\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)+\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\Rightarrow\int_{\mathrm{1}} ^{\mathrm{x}} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}}\:=\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)−\mathrm{ln}\left(\mathrm{2}\right)\:\:\left(\mathrm{c}=−\mathrm{ln2}\right) \\ $$$$\mathrm{if}\:\mathrm{x}>\mathrm{1}\:\mathrm{we}\:\mathrm{take}\:\mathrm{g}\left(\mathrm{x}\right)=\int_{\mathrm{1}} ^{\mathrm{x}} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}}\:=_{\mathrm{t}=\frac{\mathrm{1}}{\mathrm{u}}} \:\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{x}}} \:\frac{−\mathrm{du}}{\mathrm{u}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{u}}\right)}\:\:\: \\ $$$$=−\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{x}}} \:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{u}}\:=\int_{\frac{\mathrm{1}}{\mathrm{x}}} ^{\mathrm{1}\:} \:\frac{\mathrm{du}}{\mathrm{u}\left(\mathrm{u}+\mathrm{1}\right)}\:=\int_{\frac{\mathrm{1}}{\mathrm{x}}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{u}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{u}^{\mathrm{n}} \:\mathrm{du} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\frac{\mathrm{1}}{\mathrm{x}}} ^{\mathrm{1}} \:\mathrm{u}^{\mathrm{n}−\mathrm{1}} \mathrm{du}\:= \\ $$$$=\int_{\frac{\mathrm{1}}{\mathrm{x}}} ^{\mathrm{1}} \:\frac{\mathrm{du}}{\mathrm{u}}\:+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\left[\frac{\mathrm{u}^{\mathrm{n}} }{\mathrm{n}}\right]_{\frac{\mathrm{1}}{\mathrm{x}}} ^{\mathrm{1}} \\ $$$$=\mathrm{ln}\left(\mathrm{x}\right)+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }\right) \\ $$$$=\mathrm{ln}\left(\mathrm{x}\right)+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}}−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{n}} \\ $$$$=\mathrm{ln}\left(\mathrm{x}\right)−\mathrm{ln}\left(\mathrm{2}\right)+\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$=\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)−\mathrm{ln}\left(\mathrm{2}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *