Question Number 166725 by cortano1 last updated on 26/Feb/22
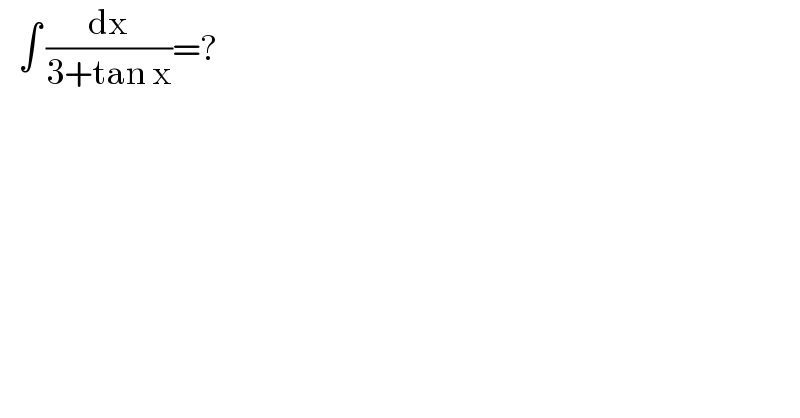
$$\:\:\:\int\:\frac{\mathrm{dx}}{\mathrm{3}+\mathrm{tan}\:\mathrm{x}}=? \\ $$
Commented by MJS_new last updated on 26/Feb/22
![∫(dx/(3+tan x))= [t=tan x → dx=(dt/(t^2 +1))]= =∫(dt/((t+3)(t^2 +1)))= =(3/(10))∫(dt/(t^2 +1))−(1/(10))∫(t/(t^2 +1))dt+(1/(10))∫(dt/(t+3))= =(3/(10))arctan t −(1/(20))ln (t^2 +1) +(1/(10))ln (t+3) = ... =(3/(10))x+(1/(10))ln ∣sin x +3cos x∣ +C](https://www.tinkutara.com/question/Q166747.png)
$$\int\frac{{dx}}{\mathrm{3}+\mathrm{tan}\:{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right]= \\ $$$$=\int\frac{{dt}}{\left({t}+\mathrm{3}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}= \\ $$$$=\frac{\mathrm{3}}{\mathrm{10}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{10}}\int\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}+\frac{\mathrm{1}}{\mathrm{10}}\int\frac{{dt}}{{t}+\mathrm{3}}= \\ $$$$=\frac{\mathrm{3}}{\mathrm{10}}\mathrm{arctan}\:{t}\:−\frac{\mathrm{1}}{\mathrm{20}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{10}}\mathrm{ln}\:\left({t}+\mathrm{3}\right)\:= \\ $$$$… \\ $$$$=\frac{\mathrm{3}}{\mathrm{10}}{x}+\frac{\mathrm{1}}{\mathrm{10}}\mathrm{ln}\:\mid\mathrm{sin}\:{x}\:+\mathrm{3cos}\:{x}\mid\:+{C} \\ $$
Commented by peter frank last updated on 27/Feb/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by som(math1967) last updated on 26/Feb/22
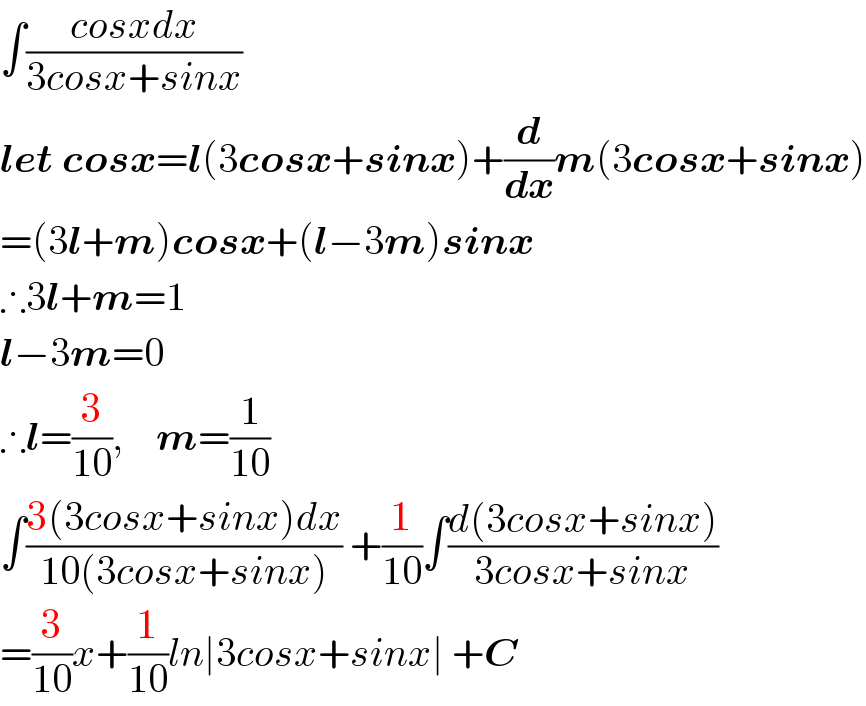
$$\int\frac{{cosxdx}}{\mathrm{3}{cosx}+{sinx}} \\ $$$$\boldsymbol{{let}}\:\boldsymbol{{cosx}}=\boldsymbol{{l}}\left(\mathrm{3}\boldsymbol{{cosx}}+\boldsymbol{{sinx}}\right)+\frac{\boldsymbol{{d}}}{\boldsymbol{{dx}}}\boldsymbol{{m}}\left(\mathrm{3}\boldsymbol{{cosx}}+\boldsymbol{{sinx}}\right) \\ $$$$=\left(\mathrm{3}\boldsymbol{{l}}+\boldsymbol{{m}}\right)\boldsymbol{{cosx}}+\left(\boldsymbol{{l}}−\mathrm{3}\boldsymbol{{m}}\right)\boldsymbol{{sinx}} \\ $$$$\therefore\mathrm{3}\boldsymbol{{l}}+\boldsymbol{{m}}=\mathrm{1}\: \\ $$$$\boldsymbol{{l}}−\mathrm{3}\boldsymbol{{m}}=\mathrm{0} \\ $$$$\therefore\boldsymbol{{l}}=\frac{\mathrm{3}}{\mathrm{10}},\:\:\:\:\boldsymbol{{m}}=\frac{\mathrm{1}}{\mathrm{10}} \\ $$$$\int\frac{\mathrm{3}\left(\mathrm{3}{cosx}+{sinx}\right){dx}}{\mathrm{10}\left(\mathrm{3}{cosx}+{sinx}\right)}\:+\frac{\mathrm{1}}{\mathrm{10}}\int\frac{{d}\left(\mathrm{3}{cosx}+{sinx}\right)}{\mathrm{3}{cosx}+{sinx}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{10}}{x}+\frac{\mathrm{1}}{\mathrm{10}}{ln}\mid\mathrm{3}{cosx}+{sinx}\mid\:+\boldsymbol{{C}} \\ $$
Answered by muneer0o0 last updated on 26/Feb/22

$$\:{I}\:=\:\int\frac{{dx}}{\mathrm{3}+\mathrm{tan}\:{x}} \\ $$$$\:\:{I}=\int\frac{\mathrm{sec}^{\mathrm{2}} {x}\:−\:\mathrm{tan}^{\mathrm{2}} {x}\:\:}{\mathrm{3}+\mathrm{tan}\:{x}}\:{dx}\: \\ $$$$\:\:{I}=\int\frac{\mathrm{sec}^{\mathrm{2}} {x}\:}{\mathrm{3}+\mathrm{tan}\:{x}}\:{dx}\:\:+\int\frac{\:−\mathrm{tan}^{\mathrm{2}} {x}\:\:\:}{\mathrm{3}+\mathrm{tan}\:{x}}\:{dx}\: \\ $$$$\:\:{I}=\int\frac{\mathrm{sec}^{\mathrm{2}} {x}\:}{\mathrm{3}+\mathrm{tan}\:{x}}\:{dx}\:\:+\int\frac{\:\mathrm{9}−\mathrm{tan}^{\mathrm{2}} {x}−\mathrm{9}\:\:\:}{\mathrm{3}+\mathrm{tan}\:{x}}\:{dx}\: \\ $$$$\:\:{I}=\int\frac{\mathrm{sec}^{\mathrm{2}} {x}\:}{\mathrm{3}+\mathrm{tan}\:{x}}\:{dx}\:\:+\int\frac{\:\cancel{\left(\mathrm{3}+\mathrm{tan}\:{x}\right)}\left(\mathrm{3}−\mathrm{tan}\:{x}\right)\:\:\:}{\cancel{\mathrm{3}+\mathrm{tan}\:{x}}}\:{dx}\:−\mathrm{9}\int\frac{{dx}}{\mathrm{3}+\mathrm{tan}\:{x}} \\ $$$$\:\:{I}=\int\frac{\mathrm{sec}^{\mathrm{2}} {x}\:}{\mathrm{3}+\mathrm{tan}\:{x}}\:{dx}\:\:+\int\left(\mathrm{3}−\mathrm{tan}\:{x}\:\right)\:{dx}\:−\mathrm{9}{I} \\ $$$$\:\mathrm{10}\:{I}=\:\mathrm{ln}\:\left(\mathrm{3}+\mathrm{tan}\:{x}\right)\:\:+\mathrm{3}{x}+\mathrm{ln}\left(\:\mathrm{cos}\:{x}\right)\:+\:{c} \\ $$$$\:\:{I}=\:\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{ln}\:\left(\mathrm{3}+\mathrm{tan}\:{x}\right)\:\:+\mathrm{3}{x}+\mathrm{ln}\left(\:\mathrm{cos}\:{x}\right)\:+\:{c}\right) \\ $$
Commented by peter frank last updated on 27/Feb/22

$$\mathrm{thank}\:\mathrm{you}\: \\ $$
