Question Number 35732 by ajfour last updated on 22/May/18
Commented by ajfour last updated on 22/May/18

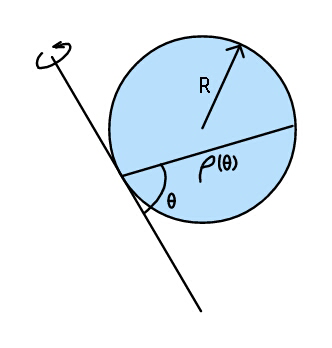
$${Find}\:{moment}\:{of}\:{inertia}\:{of}\:{disc} \\ $$$${about}\:{an}\:{axis},\:{as}\:{in}\:{figure}\:{above}, \\ $$$${if}\:{density}\:{of}\:{disc}\:{be}\:{proportional} \\ $$$${to}\:\mathrm{sin}\:\theta\:. \\ $$
Answered by ajfour last updated on 23/May/18
![chord length at angle θ is ρ= 2Rsin θ let areal density be δ=ksin θ dI=(rsin θ)^2 dm ; r being distance of a mass element from point of tangency of disc with axis of rotation. ∫dI=∫_0 ^( π) ∫_0 ^( ρ) (rsin θ)^2 (ksin θ)(rdθ)dr = k∫_0 ^( π) [(sin^3 θ)∫_0 ^( ρ) r^3 dr]dθ = k∫_0 ^( π) (sin^3 θ)((ρ^4 /4))dθ as ρ=2Rsin θ, we have I= 4kR^( 4) ∫_0 ^( π) sin^7 θdθ =−4kR^( 4) ∫_0 ^( π) (1−cos^2 θ)^3 (−sin θdθ) let cos θ =t ⇒ −sin θdθ=dt I =−4kR^( 4) ∫_1 ^( −1) (1−t^2 )^3 dt = 8R^( 2) k∫_0 ^( 1) (1−3t^2 +3t^4 −t^6 )dt =8kR^( 4) [t−t^3 +((3t^5 )/5)−(t^7 /7)]∣_0 ^1 ⇒ I=8kR^( 4) (((16)/(35))) or I= ((128kR^( 4) )/(35)) .](https://www.tinkutara.com/question/Q35752.png)
$${chord}\:{length}\:{at}\:{angle}\:\theta\:{is} \\ $$$$\:\:\:\:\rho=\:\mathrm{2}{R}\mathrm{sin}\:\theta \\ $$$${let}\:{areal}\:{density}\:{be}\:\delta={k}\mathrm{sin}\:\theta \\ $$$${dI}=\left({r}\mathrm{sin}\:\theta\right)^{\mathrm{2}} {dm}\:\:\:;\:{r}\:{being}\:{distance}\:{of} \\ $$$${a}\:{mass}\:{element}\:{from}\:{point}\:{of} \\ $$$${tangency}\:{of}\:{disc}\:{with}\:{axis}\:{of} \\ $$$${rotation}. \\ $$$$\int{dI}=\int_{\mathrm{0}} ^{\:\:\pi} \int_{\mathrm{0}} ^{\:\:\rho} \left({r}\mathrm{sin}\:\theta\right)^{\mathrm{2}} \left({k}\mathrm{sin}\:\theta\right)\left({rd}\theta\right){dr} \\ $$$$\:\:\:\:\:\:\:=\:{k}\int_{\mathrm{0}} ^{\:\:\pi} \left[\left(\mathrm{sin}\:^{\mathrm{3}} \theta\right)\int_{\mathrm{0}} ^{\:\:\rho} {r}^{\mathrm{3}} {dr}\right]{d}\theta \\ $$$$\:\:\:\:\:\:\:=\:{k}\int_{\mathrm{0}} ^{\:\:\pi} \left(\mathrm{sin}\:^{\mathrm{3}} \theta\right)\left(\frac{\rho^{\mathrm{4}} }{\mathrm{4}}\right){d}\theta \\ $$$$\:\:\:\:\:\:\:{as}\:\rho=\mathrm{2}{R}\mathrm{sin}\:\theta,\:{we}\:{have} \\ $$$$\:\:\:\:{I}=\:\mathrm{4}{kR}^{\:\mathrm{4}} \int_{\mathrm{0}} ^{\:\:\pi} \mathrm{sin}\:^{\mathrm{7}} \theta{d}\theta \\ $$$$\:\:\:\:\:\:=−\mathrm{4}{kR}^{\:\mathrm{4}} \int_{\mathrm{0}} ^{\:\:\pi} \left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \theta\right)^{\mathrm{3}} \left(−\mathrm{sin}\:\theta{d}\theta\right) \\ $$$${let}\:\:\mathrm{cos}\:\theta\:={t}\:\:\:\:\Rightarrow\:\:−\mathrm{sin}\:\theta{d}\theta={dt} \\ $$$$\:\:\:\:\:\:{I}\:=−\mathrm{4}{kR}^{\:\mathrm{4}} \int_{\mathrm{1}} ^{\:\:−\mathrm{1}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{3}} {dt} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\mathrm{8}{R}^{\:\mathrm{2}} {k}\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \left(\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} +\mathrm{3}{t}^{\mathrm{4}} −{t}^{\mathrm{6}} \right){dt} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{8}{kR}^{\:\mathrm{4}} \left[{t}−{t}^{\mathrm{3}} +\frac{\mathrm{3}{t}^{\mathrm{5}} }{\mathrm{5}}−\frac{{t}^{\mathrm{7}} }{\mathrm{7}}\right]\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\Rightarrow\:\:\:\:{I}=\mathrm{8}{kR}^{\:\mathrm{4}} \left(\frac{\mathrm{16}}{\mathrm{35}}\right) \\ $$$${or}\:\:\:\:\:\boldsymbol{{I}}=\:\frac{\mathrm{128}\boldsymbol{{kR}}^{\:\mathrm{4}} }{\mathrm{35}}\:. \\ $$
