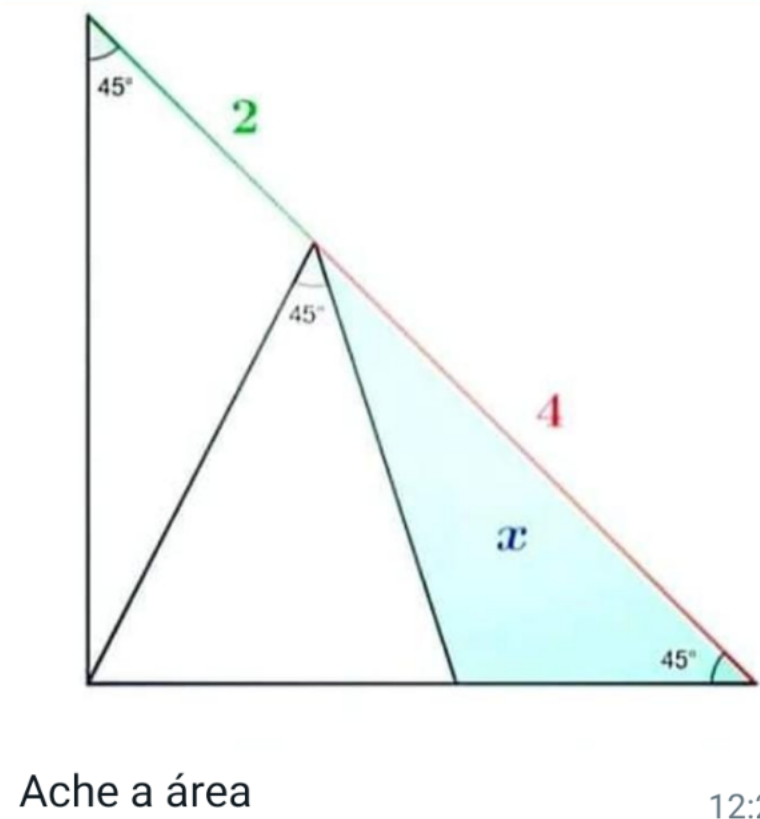
Question Number 166834 by leicianocosta last updated on 28/Feb/22
Answered by Rasheed.Sindhi last updated on 28/Feb/22
Commented by Rasheed.Sindhi last updated on 28/Feb/22
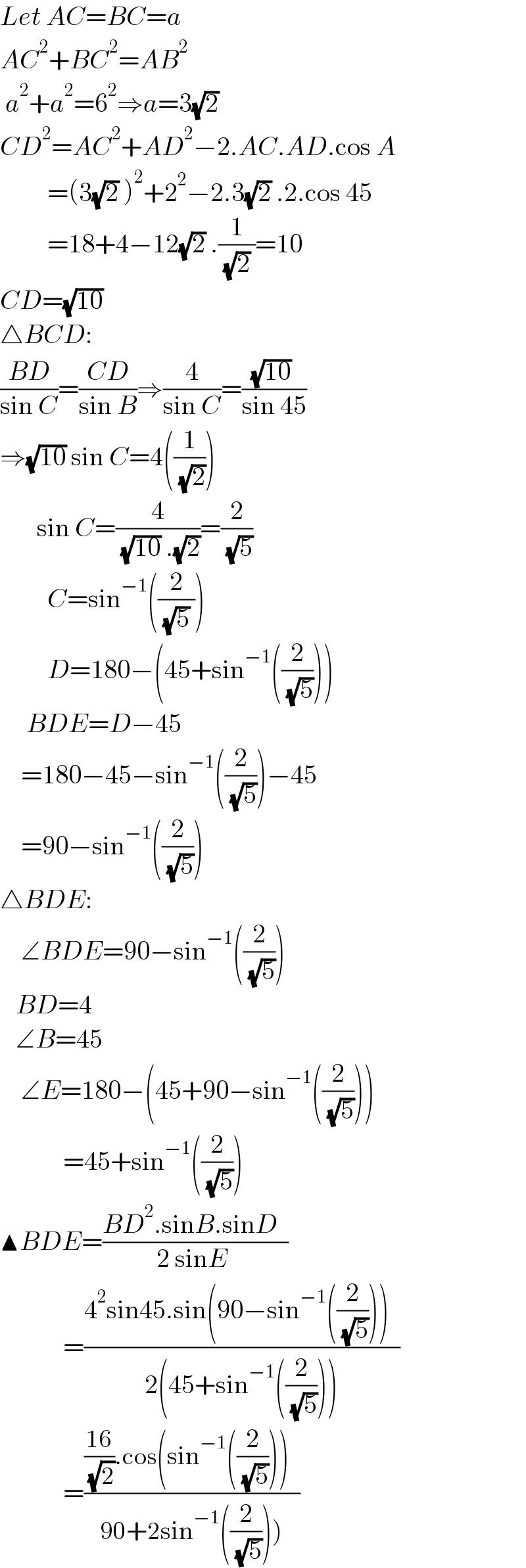
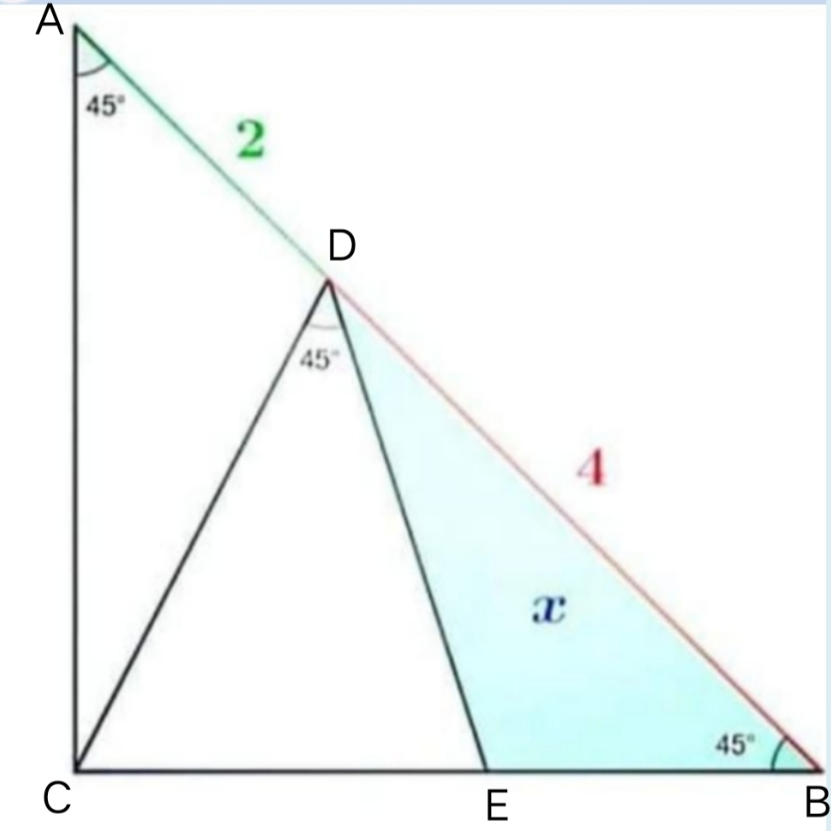
$${Let}\:{AC}={BC}={a} \\ $$$${AC}^{\mathrm{2}} +{BC}^{\mathrm{2}} ={AB}^{\mathrm{2}} \\ $$$$\:{a}^{\mathrm{2}} +{a}^{\mathrm{2}} =\mathrm{6}^{\mathrm{2}} \Rightarrow{a}=\mathrm{3}\sqrt{\mathrm{2}}\: \\ $$$${CD}^{\mathrm{2}} ={AC}^{\mathrm{2}} +{AD}^{\mathrm{2}} −\mathrm{2}.{AC}.{AD}.\mathrm{cos}\:{A} \\ $$$$\:\:\:\:\:\:\:\:\:=\left(\mathrm{3}\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} −\mathrm{2}.\mathrm{3}\sqrt{\mathrm{2}}\:.\mathrm{2}.\mathrm{cos}\:\mathrm{45} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{18}+\mathrm{4}−\mathrm{12}\sqrt{\mathrm{2}}\:.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}=\mathrm{10} \\ $$$${CD}=\sqrt{\mathrm{10}}\: \\ $$$$\bigtriangleup{BCD}: \\ $$$$\frac{{BD}}{\mathrm{sin}\:{C}}=\frac{{CD}}{\mathrm{sin}\:{B}}\Rightarrow\frac{\mathrm{4}}{\mathrm{sin}\:{C}}=\frac{\sqrt{\mathrm{10}}\:}{\mathrm{sin}\:\mathrm{45}} \\ $$$$\Rightarrow\sqrt{\mathrm{10}}\:\mathrm{sin}\:{C}=\mathrm{4}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{sin}\:{C}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{10}}\:.\sqrt{\mathrm{2}}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}} \\ $$$$\:\:\:\:\:\:\:\:\:{C}=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}\:}\right) \\ $$$$\:\:\:\:\:\:\:\:\:{D}=\mathrm{180}−\left(\mathrm{45}+\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\right)\right) \\ $$$$\:\:\:\:\:{BDE}={D}−\mathrm{45} \\ $$$$\:\:\:\:=\mathrm{180}−\mathrm{45}−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\right)−\mathrm{45} \\ $$$$\:\:\:\:=\mathrm{90}−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\right) \\ $$$$\bigtriangleup{BDE}: \\ $$$$\:\:\:\:\angle{BDE}=\mathrm{90}−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\right) \\ $$$$\:\:\:{BD}=\mathrm{4} \\ $$$$\:\:\:\angle{B}=\mathrm{45} \\ $$$$\:\:\:\:\angle{E}=\mathrm{180}−\left(\mathrm{45}+\mathrm{90}−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{45}+\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\right) \\ $$$$\blacktriangle{BDE}=\frac{{BD}^{\mathrm{2}} .\mathrm{sin}{B}.\mathrm{sin}{D}\:\:}{\mathrm{2}\:\mathrm{sin}{E}\:} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{4}^{\mathrm{2}} \mathrm{sin45}.\mathrm{sin}\left(\mathrm{90}−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\right)\right)\:\:}{\mathrm{2}\left(\mathrm{45}+\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\right)\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\frac{\mathrm{16}}{\:\sqrt{\mathrm{2}}}.\mathrm{cos}\left(\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\right)\right)\:\:}{\left.\mathrm{90}+\mathrm{2sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\right)\right)} \\ $$
Commented by Tawa11 last updated on 01/Mar/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 28/Feb/22
Commented by mr W last updated on 28/Feb/22
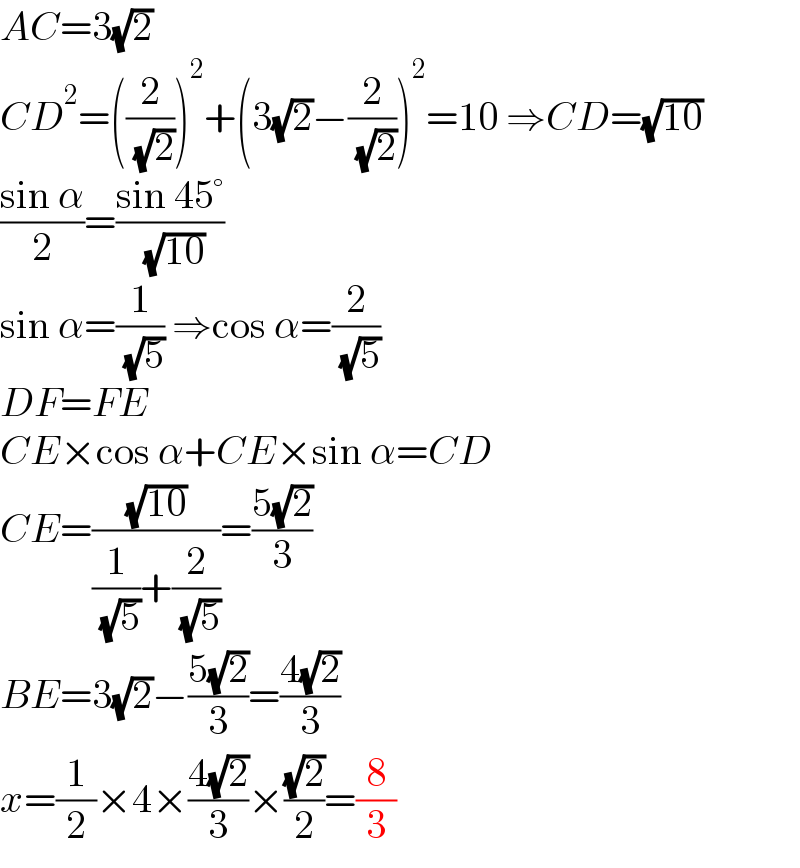
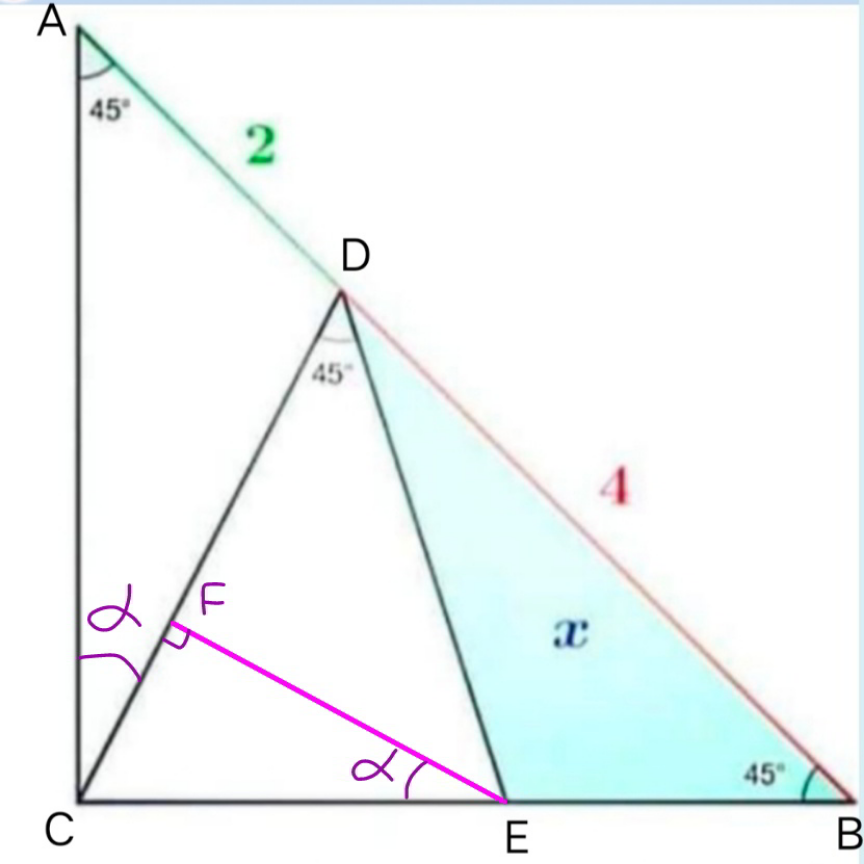
$${AC}=\mathrm{3}\sqrt{\mathrm{2}} \\ $$$${CD}^{\mathrm{2}} =\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\left(\mathrm{3}\sqrt{\mathrm{2}}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} =\mathrm{10}\:\Rightarrow{CD}=\sqrt{\mathrm{10}} \\ $$$$\frac{\mathrm{sin}\:\alpha}{\mathrm{2}}=\frac{\mathrm{sin}\:\mathrm{45}°}{\:\sqrt{\mathrm{10}}} \\ $$$$\mathrm{sin}\:\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\:\Rightarrow\mathrm{cos}\:\alpha=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}} \\ $$$${DF}={FE} \\ $$$${CE}×\mathrm{cos}\:\alpha+{CE}×\mathrm{sin}\:\alpha={CD} \\ $$$${CE}=\frac{\sqrt{\mathrm{10}}}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}}=\frac{\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$${BE}=\mathrm{3}\sqrt{\mathrm{2}}−\frac{\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{3}}=\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{4}×\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{3}}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=\frac{\mathrm{8}}{\mathrm{3}} \\ $$
Commented by Tawa11 last updated on 01/Mar/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
