Question Number 134547 by EDWIN88 last updated on 05/Mar/21
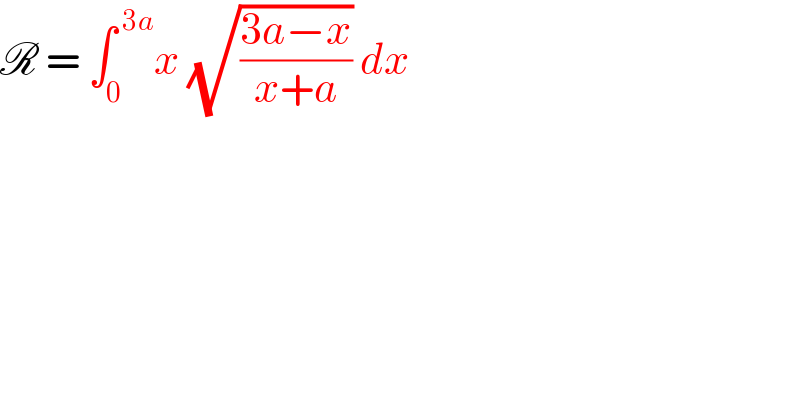
$$\mathscr{R}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{3}{a}} {x}\:\sqrt{\frac{\mathrm{3}{a}−{x}}{{x}+{a}}}\:{dx}\: \\ $$
Answered by liberty last updated on 05/Mar/21
![by change of variable let (√((3a−x)/(x+a))) =h ⇒ x=((−ah^2 +3a)/(h^2 +1)) dx = −((8ah)/((h^2 +1)^2 )) dh with → { ((x=3a→h=0)),((x=0→h=(√3))) :} R = ∫_(√3) ^( 0) (((3a−ah^2 )/(h^2 +1)))h(−((8ah)/((h^2 +1)^2 )))dh = 8a^2 ∫_0 ^( (√3)) (((h^2 (3−h^2 ))/((h^2 +1)^3 )))dh =8a^2 ∫_0 ^( (√3)) (3h−h^3 ).((h/((h^2 +1)^3 )))dh applying integration by parts with { ((u=3h−h^3 ⇒du=3−3h^2 dh)),((v=−(1/(4(h^2 +1)^2 )))) :} R = 8a^2 [−((3h−h^3 )/(4(h^2 +1)^2 ))]_0 ^(√3) +2a^2 ∫_0 ^( (√3)) (((3−3h^2 ))/((h^2 +1)^2 ))dh = 0 + 2a^2 ∫_0 ^( (√3)) (((3−3h^2 )/((h^2 +1)^2 )))dh = 6a^2 ∫_0 ^(√3) (((1−h^2 )/((h^2 +1)^2 )))dh let h = tan ϕ ⇒dh = sec^2 ϕ dϕ R = 6a^2 ∫_0 ^( π/3) (((1−tan^2 ϕ))/(sec^4 ϕ)))sec^2 ϕ dϕ = 6a^2 ∫_0 ^( π/3) (cos^2 ϕ−sin^2 ϕ)dϕ = 6a^2 ∫_0 ^( π/3) (cos 2ϕ) dϕ = 3a^2 [ sin 2ϕ ]_0 ^(π/3) = 3a^2 ×((√3)/2) = ((3a^2 (√3))/2)](https://www.tinkutara.com/question/Q134548.png)
$$\mathrm{by}\:\mathrm{change}\:\mathrm{of}\:\mathrm{variable}\: \\ $$$$\:\mathrm{let}\:\sqrt{\frac{\mathrm{3}{a}−{x}}{{x}+{a}}}\:={h}\:\Rightarrow\:{x}=\frac{−{ah}^{\mathrm{2}} +\mathrm{3}{a}}{{h}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\:{dx}\:=\:−\frac{\mathrm{8}{ah}}{\left({h}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:{dh}\:{with}\:\rightarrow\begin{cases}{{x}=\mathrm{3}{a}\rightarrow{h}=\mathrm{0}}\\{{x}=\mathrm{0}\rightarrow{h}=\sqrt{\mathrm{3}}}\end{cases} \\ $$$$\mathscr{R}\:=\:\int_{\sqrt{\mathrm{3}}} ^{\:\mathrm{0}} \left(\frac{\mathrm{3}{a}−{ah}^{\mathrm{2}} }{{h}^{\mathrm{2}} +\mathrm{1}}\right){h}\left(−\frac{\mathrm{8}{ah}}{\left({h}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\right){dh} \\ $$$$=\:\mathrm{8}{a}^{\mathrm{2}} \int_{\mathrm{0}} ^{\:\sqrt{\mathrm{3}}} \left(\frac{{h}^{\mathrm{2}} \left(\mathrm{3}−{h}^{\mathrm{2}} \right)}{\left({h}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\right){dh}\: \\ $$$$=\mathrm{8}{a}^{\mathrm{2}} \int_{\mathrm{0}} ^{\:\sqrt{\mathrm{3}}} \left(\mathrm{3}{h}−{h}^{\mathrm{3}} \right).\left(\frac{{h}}{\left({h}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\right){dh} \\ $$$$\mathrm{applying}\:\mathrm{integration}\:\mathrm{by}\:\mathrm{parts} \\ $$$$\mathrm{with}\:\begin{cases}{\mathrm{u}=\mathrm{3h}−\mathrm{h}^{\mathrm{3}} \Rightarrow\mathrm{du}=\mathrm{3}−\mathrm{3h}^{\mathrm{2}} \:\mathrm{dh}}\\{\mathrm{v}=−\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{h}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }}\end{cases} \\ $$$$\mathscr{R}\:=\:\mathrm{8}{a}^{\mathrm{2}} \:\left[−\frac{\mathrm{3}{h}−{h}^{\mathrm{3}} }{\mathrm{4}\left({h}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} +\mathrm{2}{a}^{\mathrm{2}} \int_{\mathrm{0}} ^{\:\sqrt{\mathrm{3}}} \frac{\left(\mathrm{3}−\mathrm{3h}^{\mathrm{2}} \right)}{\left(\mathrm{h}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dh} \\ $$$$=\:\mathrm{0}\:+\:\mathrm{2}{a}^{\mathrm{2}} \:\int_{\mathrm{0}} ^{\:\sqrt{\mathrm{3}}} \left(\frac{\mathrm{3}−\mathrm{3h}^{\mathrm{2}} }{\left(\mathrm{h}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\right)\mathrm{dh} \\ $$$$=\:\mathrm{6}{a}^{\mathrm{2}} \:\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \left(\frac{\mathrm{1}−\mathrm{h}^{\mathrm{2}} }{\left(\mathrm{h}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\right)\mathrm{dh} \\ $$$$\mathrm{let}\:\mathrm{h}\:=\:\mathrm{tan}\:\varphi\:\Rightarrow\mathrm{dh}\:=\:\mathrm{sec}\:^{\mathrm{2}} \varphi\:\mathrm{d}\varphi \\ $$$$\mathscr{R}\:=\:\mathrm{6}{a}^{\mathrm{2}} \int_{\mathrm{0}} ^{\:\pi/\mathrm{3}} \left(\frac{\left.\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \varphi\right)}{\mathrm{sec}\:^{\mathrm{4}} \varphi}\right)\mathrm{sec}\:^{\mathrm{2}} \varphi\:\mathrm{d}\varphi \\ $$$$=\:\mathrm{6}{a}^{\mathrm{2}} \int_{\mathrm{0}} ^{\:\pi/\mathrm{3}} \left(\mathrm{cos}\:^{\mathrm{2}} \varphi−\mathrm{sin}\:^{\mathrm{2}} \varphi\right)\mathrm{d}\varphi \\ $$$$=\:\mathrm{6}{a}^{\mathrm{2}} \int_{\mathrm{0}} ^{\:\pi/\mathrm{3}} \left(\mathrm{cos}\:\mathrm{2}\varphi\right)\:\mathrm{d}\varphi\: \\ $$$$=\:\mathrm{3}{a}^{\mathrm{2}} \:\left[\:\mathrm{sin}\:\mathrm{2}\varphi\:\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} =\:\mathrm{3}{a}^{\mathrm{2}} ×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\:\frac{\mathrm{3}{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
Answered by MJS_new last updated on 05/Mar/21
![∫x(√((3a−x)/(x+a)))dx= [t=(√((3a−x)/(x+a))) → dx=−((√((3a−x)(x+a)^3 ))/(2a))dt] =8a^2 ∫((t^2 (t^2 −3))/((t^2 +1)^3 ))dt= [Ostrogradski] =−((8a^2 t^3 )/((t^2 +1)^2 ))+8a^2 ∫(0/(t^2 +1))dt= =−((8a^2 t^3 )/((t^2 +1)^2 ))=−((√((3a−x)^3 (x+a)))/2)+C ⇒ snswer is ((3(√3))/2)a^2](https://www.tinkutara.com/question/Q134563.png)
$$\int{x}\sqrt{\frac{\mathrm{3}{a}−{x}}{{x}+{a}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\frac{\mathrm{3}{a}−{x}}{{x}+{a}}}\:\rightarrow\:{dx}=−\frac{\sqrt{\left(\mathrm{3}{a}−{x}\right)\left({x}+{a}\right)^{\mathrm{3}} }}{\mathrm{2}{a}}{dt}\right] \\ $$$$=\mathrm{8}{a}^{\mathrm{2}} \int\frac{{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{3}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}\right] \\ $$$$=−\frac{\mathrm{8}{a}^{\mathrm{2}} {t}^{\mathrm{3}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\mathrm{8}{a}^{\mathrm{2}} \int\frac{\mathrm{0}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}= \\ $$$$=−\frac{\mathrm{8}{a}^{\mathrm{2}} {t}^{\mathrm{3}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\sqrt{\left(\mathrm{3}{a}−{x}\right)^{\mathrm{3}} \left({x}+{a}\right)}}{\mathrm{2}}+{C} \\ $$$$\Rightarrow\:\mathrm{snswer}\:\mathrm{is}\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}{a}^{\mathrm{2}} \\ $$
Commented by liberty last updated on 05/Mar/21
$$\mathrm{Ostrogradsky}\:\mathrm{popular}\:\mathrm{method} \\ $$
