Question Number 101436 by bobhans last updated on 02/Jul/20
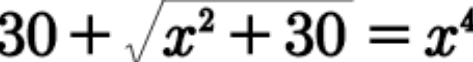
Answered by bramlex last updated on 02/Jul/20
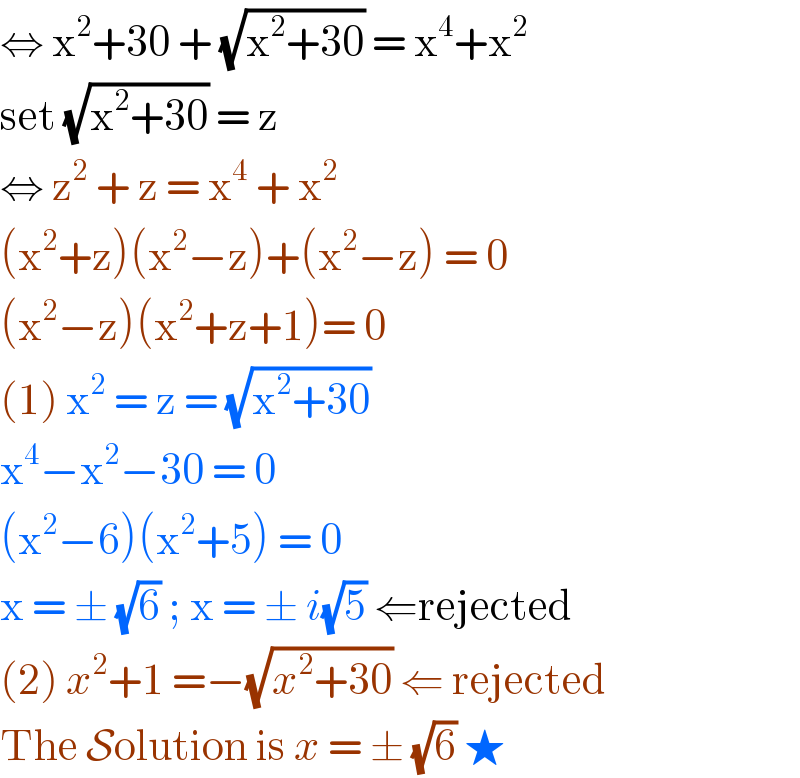
$$\Leftrightarrow\:\mathrm{x}^{\mathrm{2}} +\mathrm{30}\:+\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{30}}\:=\:\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{set}\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{30}}\:=\:\mathrm{z} \\ $$$$\Leftrightarrow\:\mathrm{z}^{\mathrm{2}} \:+\:\mathrm{z}\:=\:\mathrm{x}^{\mathrm{4}} \:+\:\mathrm{x}^{\mathrm{2}} \\ $$$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{z}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{z}\right)+\left(\mathrm{x}^{\mathrm{2}} −\mathrm{z}\right)\:=\:\mathrm{0} \\ $$$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{z}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{z}+\mathrm{1}\right)=\:\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{x}^{\mathrm{2}} \:=\:\mathrm{z}\:=\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{30}} \\ $$$$\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} −\mathrm{30}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{6}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{5}\right)\:=\:\mathrm{0}\: \\ $$$$\mathrm{x}\:=\:\pm\:\sqrt{\mathrm{6}}\:;\:\mathrm{x}\:=\:\pm\:{i}\sqrt{\mathrm{5}}\:\Leftarrow\mathrm{rejected} \\ $$$$\left(\mathrm{2}\right)\:{x}^{\mathrm{2}} +\mathrm{1}\:=−\sqrt{{x}^{\mathrm{2}} +\mathrm{30}}\:\Leftarrow\:\mathrm{rejected} \\ $$$$\mathrm{The}\:\mathcal{S}\mathrm{olution}\:\mathrm{is}\:{x}\:=\:\pm\:\sqrt{\mathrm{6}}\:\bigstar \\ $$
