Question Number 167126 by MathsFan last updated on 07/Mar/22

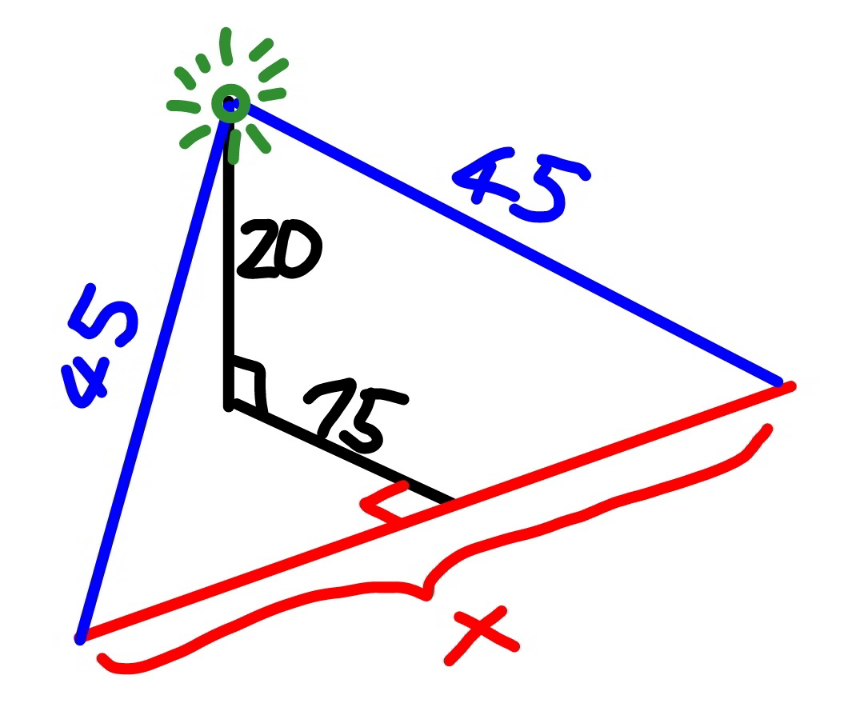
$$ \\ $$Assuming one of the WiFi towers of a building is 20km high, and has a perpendicular distance of 15km to a straight road.
Calculate the distance of the road which receives a good WiFi signal if it has a limited range of 45km
Calculate the distance of the road which receives a good WiFi signal if it has a limited range of 45km
(Calculate to four significant figures)
Commented by mr W last updated on 07/Mar/22
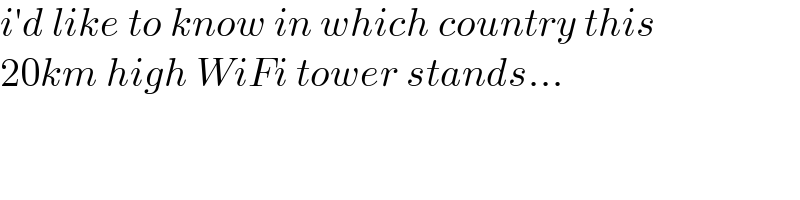
$${i}'{d}\:{like}\:{to}\:{know}\:{in}\:{which}\:{country}\:{this} \\ $$$$\mathrm{20}{km}\:{high}\:{WiFi}\:{tower}\:{stands}… \\ $$
Commented by MathsFan last updated on 07/Mar/22
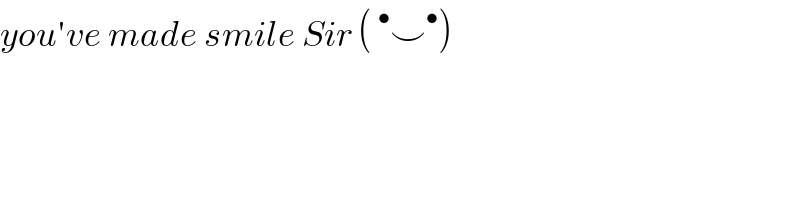
$${you}'{ve}\:{made}\:{smile}\:{Sir}\:\left(\:^{\bullet} \smile^{\bullet} \right) \\ $$
Commented by mr W last updated on 07/Mar/22
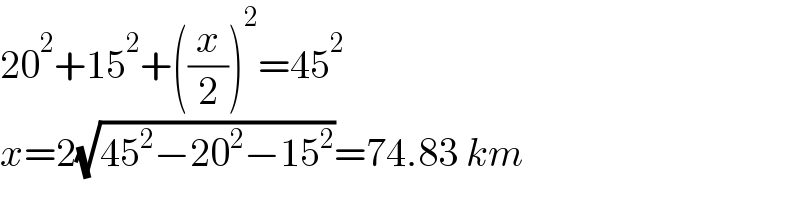
$$\mathrm{20}^{\mathrm{2}} +\mathrm{15}^{\mathrm{2}} +\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{45}^{\mathrm{2}} \\ $$$${x}=\mathrm{2}\sqrt{\mathrm{45}^{\mathrm{2}} −\mathrm{20}^{\mathrm{2}} −\mathrm{15}^{\mathrm{2}} }=\mathrm{74}.\mathrm{83}\:{km} \\ $$
Commented by TheSupreme last updated on 07/Mar/22
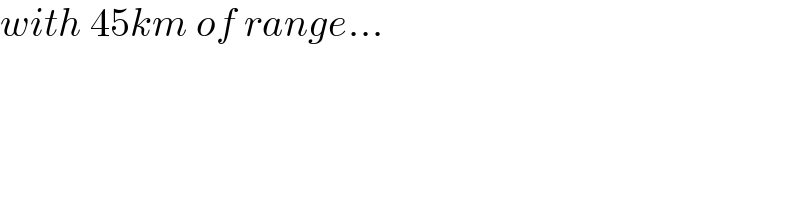
$${with}\:\mathrm{45}{km}\:{of}\:{range}… \\ $$
Commented by MathsFan last updated on 07/Mar/22

$${thank}\:{you}\:{sir} \\ $$
Commented by mr W last updated on 07/Mar/22
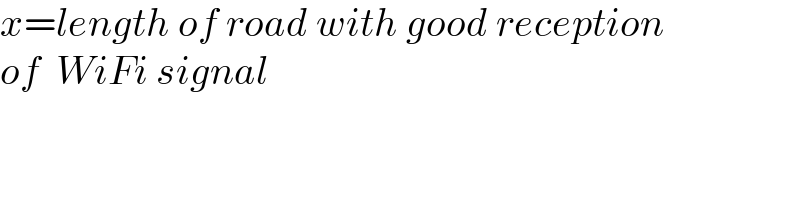
$${x}={length}\:{of}\:{road}\:{with}\:{good}\:{reception} \\ $$$${of}\:\:{WiFi}\:{signal} \\ $$
Commented by mr W last updated on 07/Mar/22
Commented by MathsFan last updated on 08/Mar/22

$${i}\:{appreciate}\:{sir} \\ $$
Commented by otchereabdullai@gmail.com last updated on 21/Mar/22
$$\mathrm{most}\:\mathrm{powerful}\:\mathrm{prof}! \\ $$
